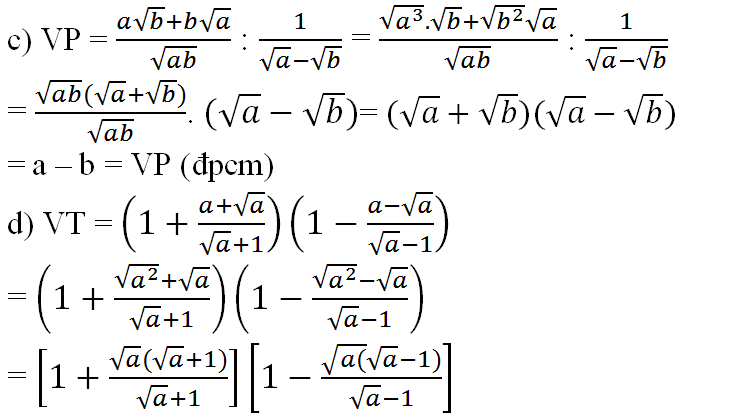Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(\left(\sqrt{a+\sqrt{b}}\ne\sqrt{a-\sqrt{b}}\right)^2\)
\(=a+\sqrt{b}\ne2\sqrt{\left(a+\sqrt{b}\right)\left(a-\sqrt{b}\right)}+a-\sqrt{b}\)
\(=2a\ne2\sqrt{a^2-b}=2\left(a\ne\sqrt{a^2}-b\right)\)
\(\Rightarrow\sqrt{a+\sqrt{b}}\ne\sqrt{a-\sqrt{b}}=\sqrt{2\left(a\ne\sqrt{a^2}-b\right)}\)
\(\Rightarrowđpcm\)
b)
\(\left(\sqrt{\frac{a+\sqrt{a^2-b}}{2}\ne}\sqrt{\frac{a-\sqrt{a^2-b}}{2}}\right)^2\)
\(=\frac{a+\sqrt{a^2-b}}{2}\ne\sqrt[2]{\frac{a+\sqrt{a^2-b}}{2}.\frac{a-\sqrt{a^2-b}}{2}}+\frac{a-\sqrt{a^2-b}}{2}\)
\(=\frac{a}{2}+\frac{\sqrt{a^2-b}}{2}\ne\sqrt[2]{\frac{a^2-a^2+b}{2.2}}+\frac{a}{2}-\frac{\sqrt{a^2-b}}{2}\)
\(=a\ne2\frac{\sqrt{b}}{2}=a\ne\sqrt{b}\)
\(\Rightarrow\sqrt{\frac{a+\sqrt{a^2-b}}{2}}\ne\sqrt{\frac{a-\sqrt{a^2-b}}{2}}=\sqrt{a\ne\sqrt{b}}\)
\(\Rightarrowđpcm\)

Lời giải:
Đặt \((\sqrt{a}, \sqrt{b}, \sqrt{c})=(x,y,z)\). Bài toán trở thành
Cho $x,y,z$ dương thỏa mãn \(y^2\neq z^2; x+y\neq z; x^2+y^2=(x+y-z)^2\)
CMR: \(\frac{x^2+(x-z)^2}{y^2+(y-z)^2}=\frac{x-z}{y-z}\)
--------------------------------------------------
Ta có:
\(x^2+y^2=(x+y-z)^2=[y+(x-z)]^2\)
\(\Leftrightarrow x^2+y^2=y^2+(x-z)^2+2y(x-z)\)
\(\Leftrightarrow x^2=(x-z)^2+2y(x-z)\)
\(\Leftrightarrow x^2+(x-z)^2=2(x-z)^2+2y(x-z)=2(x-z)(x-z+y)\)
Tương tự:
\(y^2+(y-z)^2=2(y-z)^2+2x(y-z)=2(y-z)(y-z+x)\)
Do đó: \(\frac{x^2+(x-z)^2}{y^2+(y-z)^2}=\frac{2(x-z)(x-z+y)}{2(y-z)(y-z+x)}=\frac{x-z}{y-z}\)
Ta có đpcm.

a) \(\dfrac{\sqrt{a}+\sqrt{b}}{2\sqrt{a}-2\sqrt{b}}-\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{a}+2\sqrt{b}}-\dfrac{2b}{b-a}\)
=\(\dfrac{\left(\sqrt{a}+\sqrt{b}\right)^2-\left(\sqrt{a}-\sqrt{b}\right)^2+4b}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
=\(\dfrac{a+2\sqrt{ab}+b-a+2\sqrt{ab}-b+4b}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
=\(\dfrac{4\sqrt{ab}+4b}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}=\dfrac{4\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
=\(\dfrac{2\sqrt{b}}{\sqrt{a}-\sqrt{b}}\)(đpcm)

1) \(VT=\frac{\sqrt{a}+\sqrt{b}}{2\left(\sqrt{a}-\sqrt{b}\right)}-\frac{\sqrt{a}-\sqrt{b}}{2\left(\sqrt{a}+\sqrt{b}\right)}+\frac{2b}{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\frac{\left(\sqrt{a}+\sqrt{b}\right)^2-\left(\sqrt{a}-\sqrt{b}\right)^2+4b}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)\(=\frac{a+2\sqrt{ab}+b-a+2\sqrt{ab}-b+4b}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\frac{4\sqrt{ab}+4b}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}\)
\(=\frac{4\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}{2\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}=\frac{2\sqrt{b}}{\sqrt{a}-\sqrt{b}}=VP\)(ĐPCM)
2) \(VT=\text{[}\frac{\left(\sqrt{a}+\sqrt{b}\right)\left(a+b-\sqrt{ab}\right)}{\left(\sqrt{a}+\sqrt{b}\right)}-\sqrt{ab}\text{]}.\frac{\left(\sqrt{a}+\sqrt{b}\right)^2}{\left(a-b\right)^2}\)
\(=\frac{\left(a+b-\sqrt{ab}-\sqrt{ab}\right)\left(\sqrt{a}+\sqrt{b}\right)^2}{\left(a-b\right)^2}\)\(=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{a}+\sqrt{b}\right)^2}{\left(a-b\right)^2}=\frac{\left(a-b\right)^2}{\left(a-b\right)^2}=1=VP\)(ĐPCM)
4) \(VT=\left(1+\frac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\frac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)\(=\left(1+\frac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(1-\frac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a=VP\)(ĐPCM)