Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

10.xếp ba đường thẳng thẳng hàng a,b,c.hai đường thẳng a,b song song với nhau
A.A vuống góc C cùng cắt C
B.A vuống góc C và B vuông góc C
C.A cắt C và A vuông góc C
11.chứng minh định lí là:
Adùng lập luận để từ giả thuyết suy ra kết luận
Bdùng hình vẽ để suy ra kết luận
Cdùng lập luân để từ kết luận suy ra giải thuyết
Ddùng đo đạt trực tiếp để suy ra kết lận
D.a vuông góc c và a cắt c

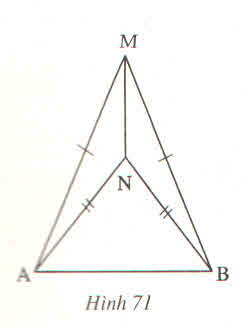
Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).
bạn làm sai chỗ Kết luận: tg AMN = tg BMN VÌ ngta nói chứng minh góc chứ ko phải tg

a/ Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau
b/ GT: Nếu một đường thẳng cắt hai đường thẳng song song
KL: thì hai góc so le trong bằng nhau

\(\frac{3x-y}{x+y}=\frac{3}{4}\)
\(\Leftrightarrow4\left(3x-y\right)=3\left(x+y\right)\)
\(\Leftrightarrow12x-4y=3x+3y\)
\(\Leftrightarrow12x-4y-3x-3y=0\)
\(\Leftrightarrow9x-7y=0\)
\(\Leftrightarrow9x=7y\Leftrightarrow\frac{x}{7}=\frac{y}{9}\)

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)
Chứng minh định lý là dùng lập luận để từ giả thiết suy ra kết luận
Chọn đáp án A.