Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
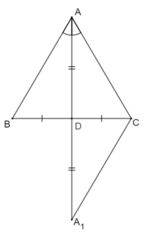
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ 
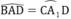(hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
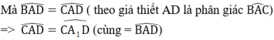
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
- Giả sử AD vừa là đường trung tuyến, vừa là đường phân giác của tam giác ABC.
Ta cần chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 sao cho DA1 = AD.
- ∆ADB và ∆A1DC có
AD = DA1 (cách vẽ)
BD = CD (do D là trung điểm BC)
Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7
⇒ ∆ADB = ∆A1DC (c.g.c)
⇒ Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7 (hai góc tương ứng), AB = A1C (hai cạnh tương ứng) (1)
Giải bài 42 trang 73 SGK Toán 7 Tập 2 | Giải toán lớp 7
⇒ ∆ACA1 cân tại C ⇒ AC = A1C (2)
Từ (1) và (2) ⇒ AB = AC.
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
Giả sử ∆ABC có AD là phân giác và DB = DC, ta chứng minh ∆ABC cân tại A
Kéo dài AD một đoạn DA1 = AD
Ta có: ∆ADC = ∆A1DC (c.g.c)
Nên
mà (gt)
=>
=> ∆ACA1 cân tại C
Ta lại có: AB = A1C ( ∆ADB = ∆A1DC)
AC = A1C ( ∆ACA1 cân tại C)
=> AB = AC
Vậy ∆ABC cân tại A
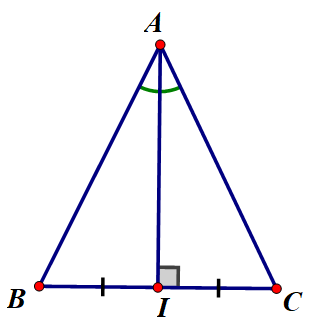
Xét tam giác ABC có AI là đường trung trực vừa là đường phân giác
vì AI là đường trung trực nên AI vuông góc với BC và I là trung điểm cuả BC
xét 2 tam giác vuông ABI và tam giác vuông ACI có;
IA chung
góc BAI=gócCAI (do AI là phân giác)
do đó tam giác BAI =tam giác CAI
suy ra AB=AC (2 cạnh tương ứng)
suy ra tam giác ABC cân tại A (định nghĩa tam giác cân)
Hướng dẫn:
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC
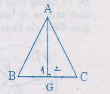
Xét hai tam giác vuông HAB và HAC có:
HB = HC
ˆH1=ˆH2H1^=H2^ = 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên
AH ⊥ BC và HB = HC
Xét hai tam giác vuông HAB và HAC có:
HB = HC
ˆH1=ˆH2H1^=H2^ = 900
AH: cạnh chung
Nên ∆HAB = ∆HAC => AB = AC
Vậy ∆ABC cân tại A
ướng dẫn:
Gọi M, N, E là giao điểm của AG, BG, CG với BC, CA, AB.
Vì G là trọng tâm của ∆ABC nên
GA = 2323AM; GB = 2323BN; GC = 2323CE (1)
Vì ∆ABC đều nên ba đường trung tuyến ứng với ba cạnh BC, CA, AB bằng nhau
=> AM = BN = CE (2)
Từ (1), (2) => GA = GB = GC
Gọi M, N, E là giao điểm của AG, BG, CG với BC, CA, AB.
Vì G là trọng tâm của ∆ABC nên
GA = 2323AM; GB = 2323BN; GC = 2323CE (1)
Vì ∆ABC đều nên ba đường trung tuyến ứng với ba cạnh BC, CA, AB bằng nhau
=> AM = BN = CE (2)
Từ (1), (2) => GA = GB = GC
A B C D
Chứng minh :
Giả sử \(\triangle ABC\) có AD là đường trung tuyến ứng với BC và \(DA=\frac{1}{2}BC\).
\(\Rightarrow AD=BD=CD\)
\(+AD=BC\Rightarrow\triangle ADC\text{ cân tại D}\)
\(\Rightarrow\widehat{A_1}=\widehat{C}\)
\(+AD=BD\Rightarrow\triangle ABD\text{ cân tại D}\)
\(\Rightarrow\widehat{A_2}=\widehat{B}\)
\(\Rightarrow\widehat{A_1}+\widehat{A_2}=\widehat{B}+\widehat{C}\)
\(\Rightarrow\widehat{A}=\widehat{B}+\widehat{C}\)
Trong \(\triangle ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{A}=\widehat{B}+\widehat{C}=\frac{180^0}{2}=90^0\)
hay \(\triangle ABC\) vuông tại A (đpcm)
cho em giải khác nhé
A B C D H G
D thuộc phân giác góc A suy ra DH = DG ( tính chất tia phân giác của một góc )
xét hai tam giác vuông BHD và CGD có
DH = DG ( cmt)
DB = DC ( gt)
do đó tam giác BHD = tam giác CGD ( cạnh huyền - góc nhọn )
suy ra góc B = góc C ( 2 góc tương ứng )
tam giác ABC có góc B = góc C suy ra tam giác ABC cân tại A
Giả sử ∆ABC có AD là phân giác ˆBACBAC^ và DB = DC, ta chứng minh ∆ABC cân tại A
Kéo dài AD một đoạn DA1 = AD
Ta có: ∆ADC = ∆A1DC (c.g.c)
Nên ˆBAD=ˆCA1DBAD^=CA1D^
mà ˆBAD=ˆCADBAD^=CAD^ (gt)
=> ˆCAD=ˆCA1DCAD^=CA1D^
=> ∆ACA1 cân tại C
Ta lại có: AB = A1C ( ∆ADB = ∆A1DC)
AC = A1C ( ∆ACA1 cân tại C)
=> AB = AC
Vậy ∆ABC cân tại A
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân