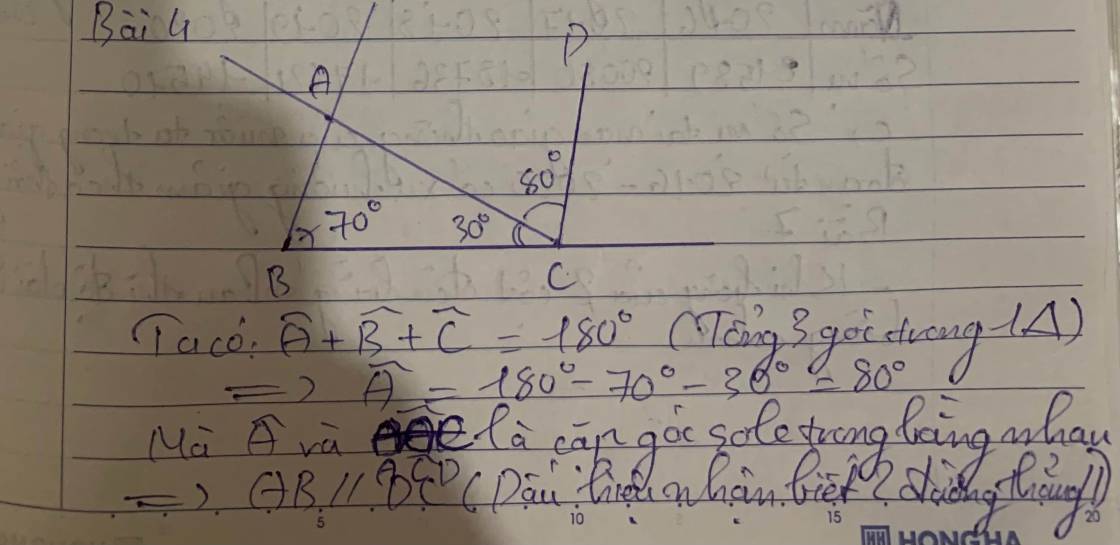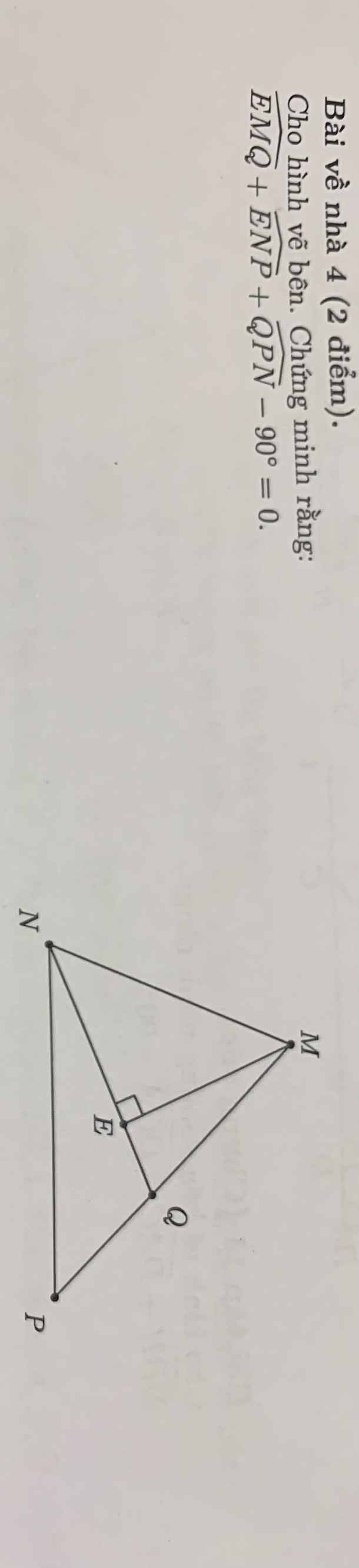Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

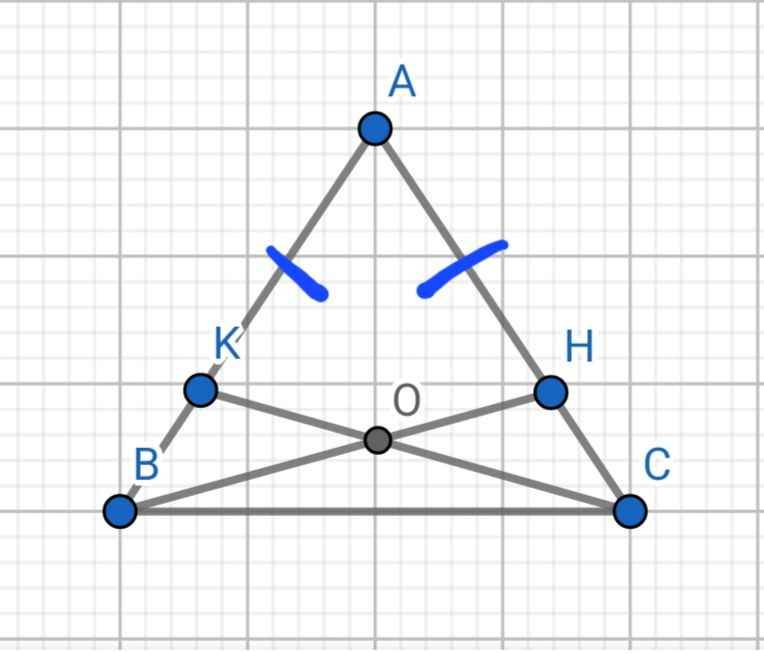
#\(N\)
`a,` Xét Tam giác `MPH` và Tam giác `MQH` có:
`MP = MQ (g``t)`
`MH` chung
\(\widehat{MHP}=\widehat{MHQ}=90^0\)
`=>` Tam giác `MPH =` Tam giác `MQH (ch - cgv)`
`=>`\(\widehat{MPH}=\widehat{MQH}\) `( 2` góc tương ứng `)`
`b,` Vì Tam giác `MPH =` Tam giác `MQH (a)`
`=>` \(\widehat{PMH}=\widehat{QMH}\) `( 2` góc tương ứng `)`
`=> MH` là tia phân giác của \(\widehat{PMQ}\)
`c,` Ta có: \(\widehat{MPH}=\widehat{MQH}=50^0\) `(CMT)`
Xét Tam giác `MQH` có:
\(\widehat{MHQ}+\widehat{MQH}+\widehat{QMH}=180^0\) `(`đlí tổng `3` góc trong `1` tam giác `)`
\(90^0+50^0+\widehat{QMH}=180^0\)
`->`\(\widehat{QMH}=180^0-90^0-50^0=40^0\)

Bài 1:
Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
KA=KH
=>ΔBAK=ΔBHK
=>BA=BH
mà KA=KH
nên BK là trung trực của AH
=>BK vuông góc AH

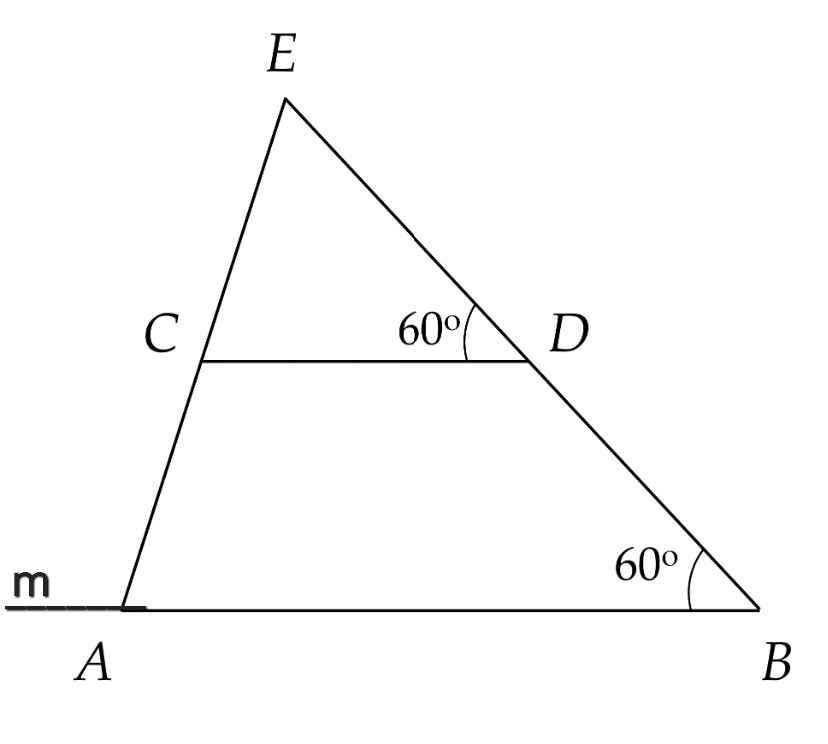
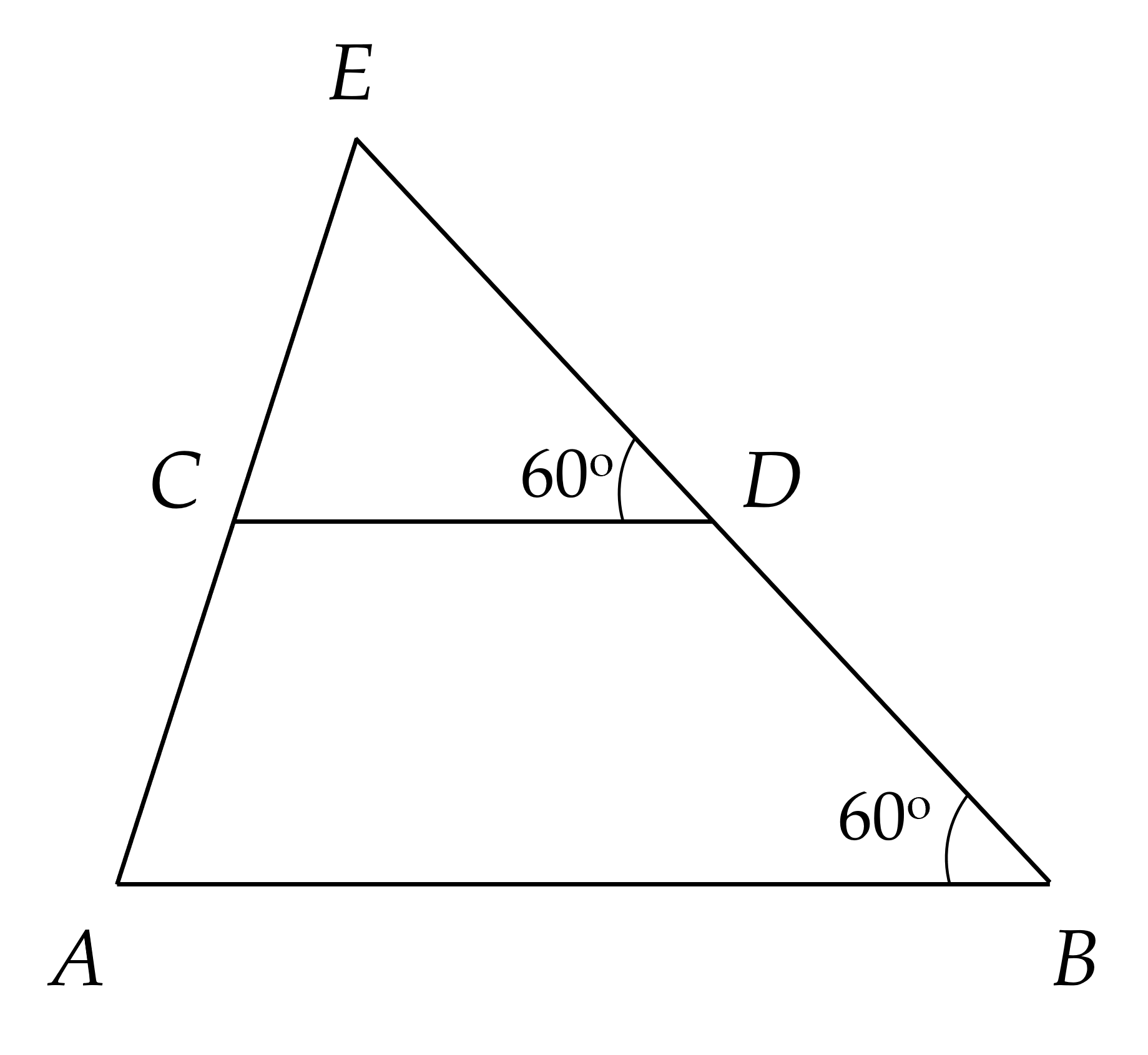
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰

Xét ∆ABC và ∆DBC có:
AB = BD
Góc ABC = góc CBD
Góc BAC = góc BDC
=> ∆ABC = ∆DBC

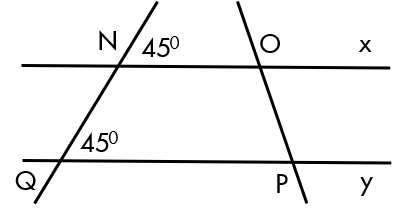
ta có góc QNO = 1800 - 450 = 1350
vì tổng 4 góc của một tứ giác bằng 3600
xét tứ giác QNOP
ta có góc NOP + góc QPO = 3600 - ( 450 + 1350) = 1800 (đpcm)

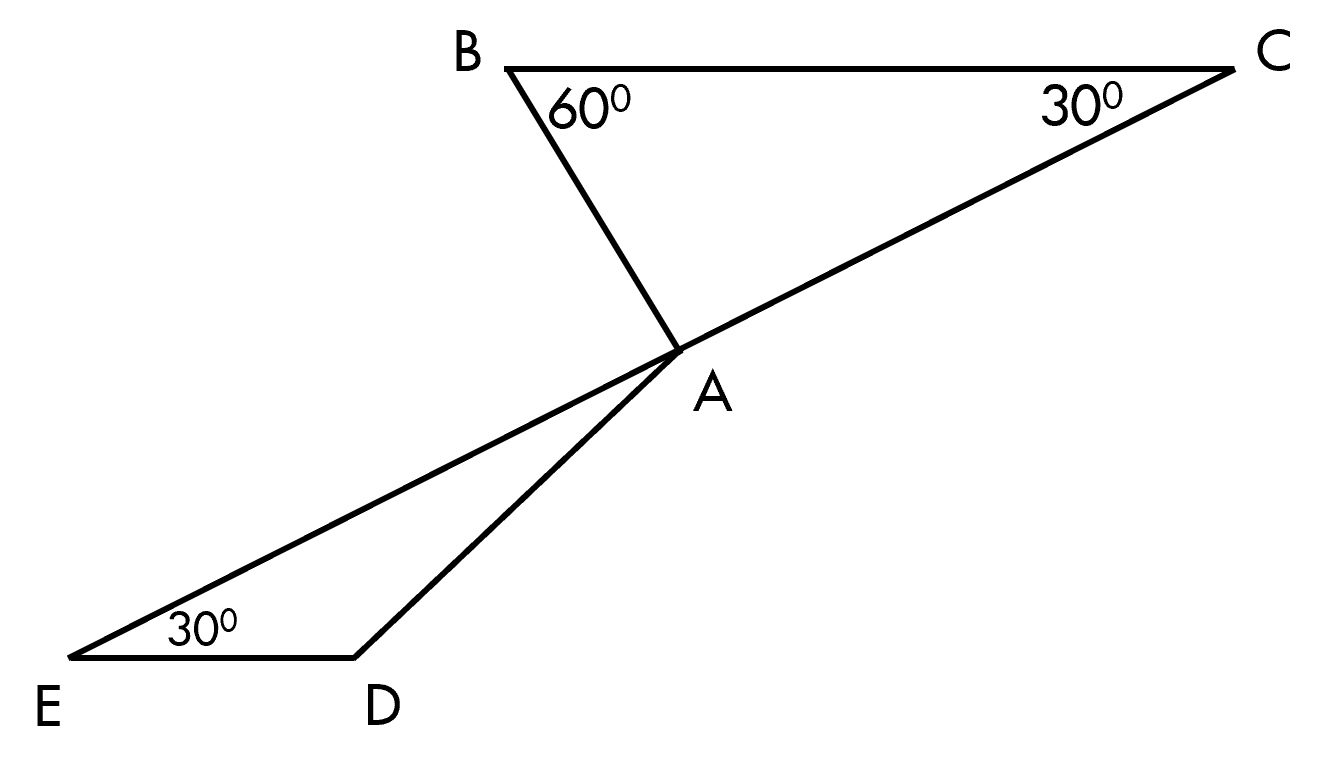
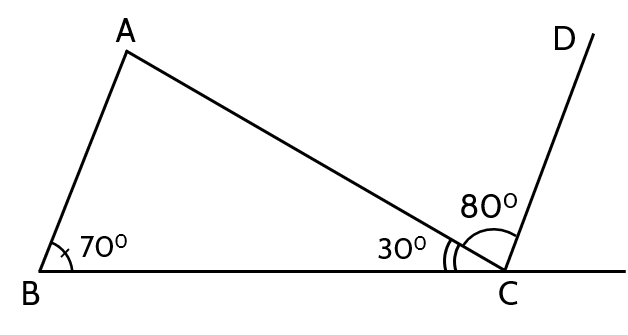
a/
\(\widehat{BCE}=\widehat{CED}=30^o\)
Hai góc trên ở vị trí sole trong => BC//DE
b/
Ta có
BC//DE (cmt) \(\Rightarrow\widehat{AFB}=180^o-\widehat{EDF}\) (Hai góc trong cùng phía bù nhau)
\(\Rightarrow\widehat{AFB}=180^o-135^o=45^o\)

Xét tg ABC có
\(\widehat{BAC}=180^o-\widehat{ABC}-\widehat{ACB}\) (tổng các góc trong của 1 tg \(=180^o\) )
\(\Rightarrow\widehat{BAC}=180^o-70^o-30^o=80^o=\widehat{ACD}\)
Hai góc \(\widehat{BAC}=\widehat{ACD}\) ở vị trí so le trong => AB//CD

\(a)\hept{\begin{cases}\text{Ta có:}\widehat{A_4}=\widehat{B_2}=110^0\\\text{Mà chúng so le trong}\end{cases}}\)
\(\Rightarrow a//b\)
\(b)\hept{\begin{cases}\text{Ta có:}c\perp a\left(gt\right)\\\text{Mà }a//b\left(cmt\right)\end{cases}}\)
\(\Rightarrow c\perp b\)
\(c)\text{Ta có:}\widehat{B_1}+\widehat{B_2}=180^0\left(\text{kề bù}\right)\)
\(\Rightarrow\widehat{B_1}=180^0-\widehat{B_2}\)
\(\Rightarrow\widehat{B_1}=180^0-110^0=70^0\)
\(\text{Ta có:}\widehat{B_1}=\widehat{B_3}=70^0\left(\text{đối đỉnh}\right)\)
\(\text{Ta có:}\widehat{B_3}=\widehat{C_3}\left(\text{Đồng vị}\right)\)
\(\Rightarrow\widehat{B_3}=\widehat{C_3}=70^0\)
a) Ta có: {ˆA4=110∘ˆB2=110∘⇒ˆA4=ˆB2=110∘{A4^=110∘B2^=110∘⇒A4^=B2^=110∘.
Mà hai góc ờ vị trí so le trong ⇒⇒ a//ba//b.
b) Ta có: {c⊥aa//b⇒c⊥b{c⊥aa//b⇒c⊥b
c) Vì a//b⇒ˆA4+ˆB1=180∘a//b⇒A4^+B1^=180∘
Mà hai góc ở vị trí trong cùng phía ⇒ˆB1=180∘−ˆA4=70∘⇒B1^=180∘−A4^=70∘.
Vì b⊥cb⊥c; e⊥ce⊥c và b//eb//e
⇒ˆB2=ˆC2=110∘⇒B2^=C2^=110∘ (hai góc ở vị trí đồng vị)
Ta có ˆC2C2^ và ˆC3C3^ là hai góc kề bù ⇒ˆC2+ˆC3=180∘⇒C2^+C3^=180∘
⇒ˆC3=180∘−ˆC2=70∘⇒C3^=180∘−C2^=70∘.

Do tam giác MQE vuông tại E \(\Rightarrow\widehat{EMQ}+\widehat{EQM}=90^0\) (1)
Mà \(\widehat{EQM}\) là góc ngoài của tam giác NPQ, theo tính chất góc ngoài của tam giác:
\(\widehat{EQM}=\widehat{ENP}+\widehat{QPN}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\widehat{EMQ}+\widehat{ENP}+\widehat{QPN}=90^0\)
\(\Rightarrow\widehat{EMQ}+\widehat{ENP}+\widehat{QPN}-90^0=0\)