Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
\(\widehat{AOM}=\stackrel\frown{AM}\)
\(\widehat{BOM}=\stackrel\frown{BM}\)
mà \(\widehat{AOM}=\widehat{BOM}\)
nên \(\overrightarrow{MA}=\stackrel\frown{MB}\)

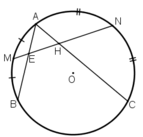
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 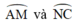
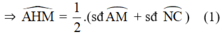
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 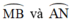
+ Do M và N là điểm chính giữa của cung A B ⏜ v à A C ⏜
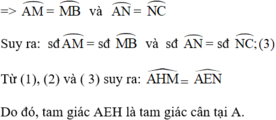

+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung ![]()
![]()
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung
là góc có đỉnh bên trong đường tròn chắn hai cung 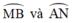

Kiến thức áp dụng
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

sđ cung AD=sđ cung AC+sđ cung CD
sđ cung DB=sđ cung DE+sđ cung EB
mà sđ cung AC=sđ cung DE và sđ cung CD=sđ cung EB
nên sđ cung AD=sđ cung DB
=>DA=DB
mà OA=OB
nên OD là đường trung trực của AB
=>OD⊥AB
Ta có: sđ cung DC=sđ cung DE
=>DC=DE
mà OC=OE
nên OD là đường trung trực của CE
=>OD⊥CE
mà OD⊥AB
nên CE//AB
Xét tứ giác CQME có
O là trung điểm chung của CM và QE
=>CQME là hình bình hành
=>CE//QM
mà CE//AB
nên AB//QM
=>ABMQ là hình thang
=>\(\hat{BAQ}+\hat{AQM}=180^0\) (1)
Xét (O) có A,B,M,Q cùng thuộc một đường tròn theo thứ tự
nên ABMQ là tứ giác nội tiếp
=>\(\hat{BAQ}+\hat{BMQ}=180^0\) (2)
Từ (1),(2) suy ra \(\hat{AQM}=\hat{BMQ}\)
=>ABMQ là hình thang cân
=>AM=BQ
Ta có: sđ cung CD=sđ cung DE
=>\(\hat{COD}=\hat{DOE}\)
mà \(\hat{COD}=\hat{NOM}\) (hai góc đối đỉnh)
và \(\hat{DOE}=\hat{QON}\) (hai góc đối đỉnh)
nên \(\hat{NOM}=\hat{QON}\)
Xét (O) có
\(\hat{NOM}\) là góc ở tâm chắn cung NM
\(\hat{QON}\) là góc ở tâm chắn cung QN
\(\hat{NOM}=\hat{QON}\)
Do đó: sđ cung NM=sđ cung QN
=>NM=QN