Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Biến đổi vế trái:
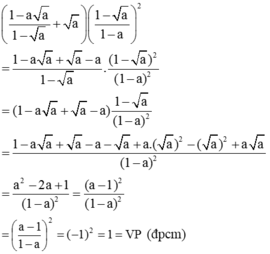
b) Biến đổi vế trái:
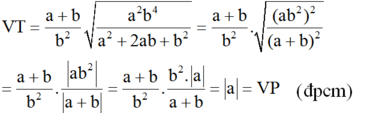
( v ì a + b > 0 n ê n | a + b | = a + b ; b 2 > 0 )

Biến đổi vế trái:
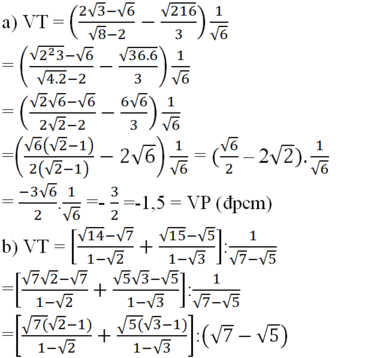
= (-√7 - √5)(√7 - √5)
= -(√7 + √5)(√7 - √5)
= -(7 - 5) = -2 = VP (đpcm)
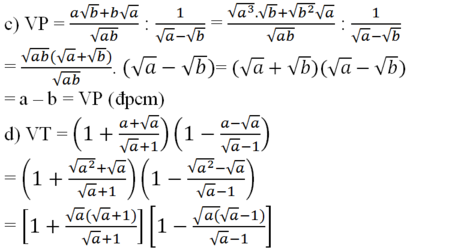
= (1 + √a)(1 - √a)
= 1 - (√a)2 = 1 - a = VP (đpcm)

\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)

Biến đổi vế trái:
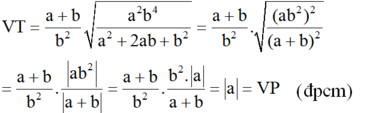
(vì a + b > 0 nên |a + b| = a + b; b2 > 0)

a) Ta có: \(\left(a-1\right)^2\ge0\forall a\)
\(\Leftrightarrow a^2-2a+1\ge0\forall a\)
\(\Leftrightarrow a^2+2a+1\ge4a\forall a\)
\(\Leftrightarrow\left(a+1\right)^2\ge4a\)(đpcm)

<=> \(a+b\ge2\sqrt{ab}\)
<=> \(a+b-2\sqrt{ab}\ge0\)
<=. \(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\)(luôn đúng )
dấu = khi a=b

a) Có: \(\left(a-1\right)^2\ge0,\forall a\)
\(\Leftrightarrow a^2-2a+1\ge0\)
\(\Leftrightarrow a^2+2a+1\ge4a\)
\(\Leftrightarrow\left(a+1\right)^2\ge4a\)
=>đpcm
b) Áp dụng bđt trên ta có:
\(\left(a+1\right)^2\ge4a\) (1)
\(\left(b+1\right)^2\ge4b\) (2)
\(\left(c+1\right)^2\ge4c\) (3)
Nhân vế vs vế (1) ; (2);(3) ta đc:
\(\left(a+1\right)^2\left(b+1\right)^2\left(c+1\right)^2\ge4a\cdot4b\cdot4c=64abc=64\)
\(\Rightarrow\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge8\)

ôi dào !dễ ợt ! cô em mới cho học ngày hôm qua !k đi rùi em trình bày cho cách làm !
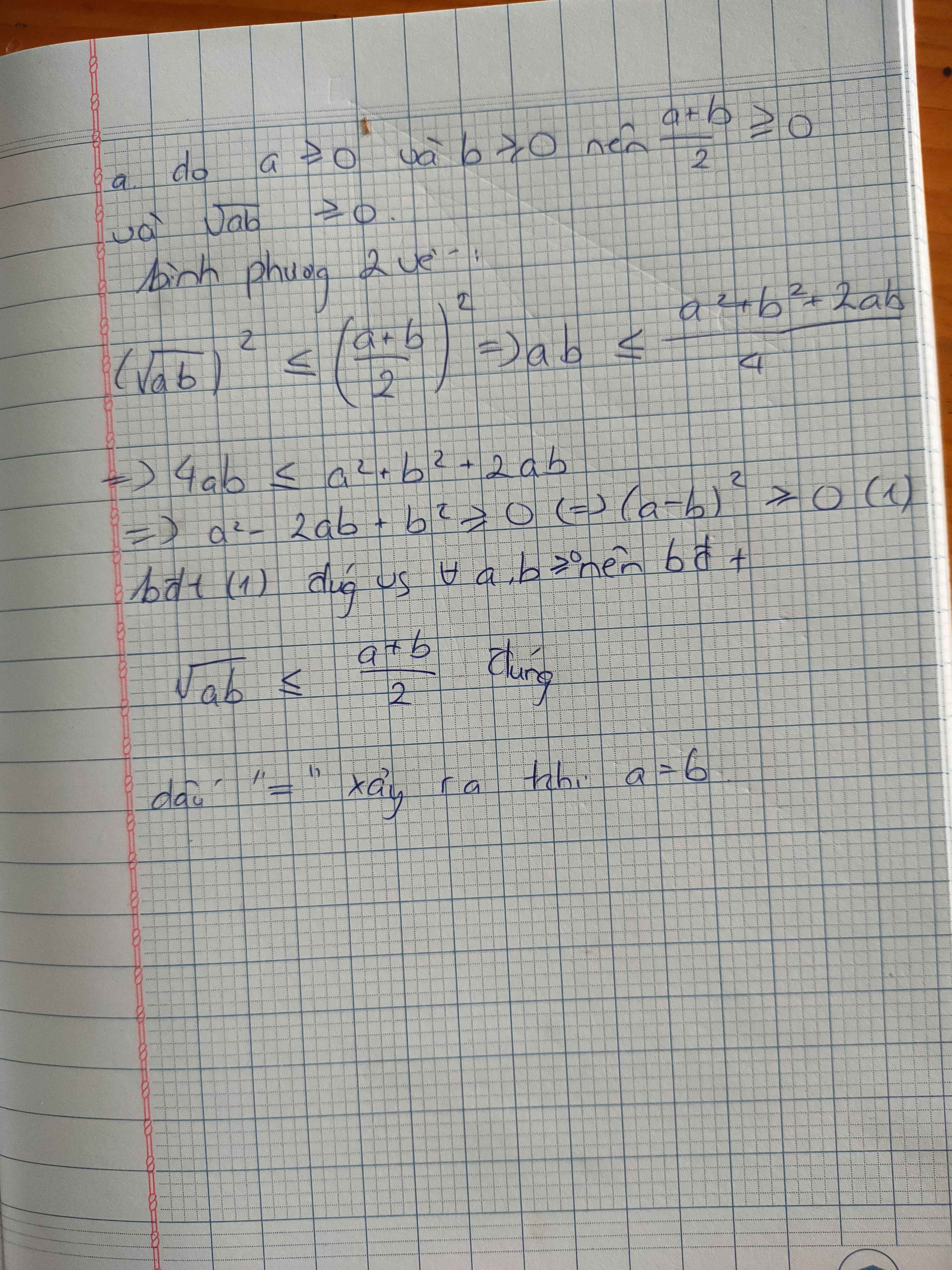
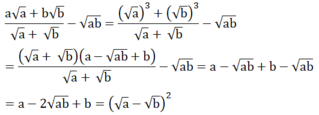
Với a > 0; b > 0 ta có: