K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SS
20 tháng 7 2016
Vật ở VTCB lò xo giãn ra một đoạn: \(\Delta l\)
\(\Rightarrow\Delta l=\frac{g}{\omega^2}\Leftrightarrow\omega\sqrt{\frac{g}{\Delta l}}\)
Tần số của con lắc lò xo:
\(\Rightarrow f=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{g}{\Delta l}}\)
8 tháng 12 2016
R1 + R2 = U2/P => U=120 V
R1R2 =(ZL-ZC)2=5184
Cos$1 = R1/(R12+R1R2)0.5=0.6
Cos$2=R2/(R22+R1R2)0.5=0.8
HD
Hà Đức Thọ
Admin
9 tháng 12 2016
Độ lệch pha giữa u và i là: \(\varphi = \dfrac{\pi}{3}\)
Công suất tiêu thụ của đoạn mạch: \(P=U.I.\cos\varphi=100.1.\cos\dfrac{\pi}{3}=50W\)
HD
Hà Đức Thọ
Admin
26 tháng 6 2016
Công thức (1) và (2) đều đúng em nhé. Nhưng em nói I và cosφ là một nên có chung công thức là không đúng trong trường hợp này.
Vì trong trường hợp (1) có suất điện động E thay đổi theo n.
26 tháng 6 2016
I = E/Z, trong trường hợp này E thay đổi theo tốc độ quay n bạn nhé.
VT
1 tháng 3 2019
+ Chứng minh f = n.p
Giả sử phần cảm có p nam châm (p cực Bắc và p cực Nam), quay với tần số n vòng/s.
Khi roto quay, đầu trên một cực Bắc quay qua một cuộn dây, rồi đến cực Nam, sau đó đến cực Bắc thứ hai.
Từ thông qua một cuộn dây biến thiên tuần hoàn với chu kì bằng thời gian để một cực Bắc đi từ một cuộn dây đến cuộn dây kế tiếp theo.
Trong một chu kì quay của roto, có p lần chu kì của dòng cảm ứng, ta có:
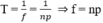
+ Áp dụng tính f: n = 600 vòng/phút = 10 vòng/s; p = 5 cặp cực
→ f = n.p = 10.5 = 50Hz
Chứng minh Udây = √3Upha
Ta có: Udây = U13 = U12 = U23; Upha = UO1 = UO2 = UO3 là các giá trị hiệu dụng của hiệu điện thế pha.
Dùng giản đồ vectơ
Hiệu điện thế dây từ A2 đến A1 là: u12 = u1O + uO2 = u1O – u2O → U1O→ - U2O→ = U12→
Vì u2O, u1O là 2 nguồn xoay chiều cùng biên độ và lệch pha nhau 2π/3
Theo quy tắc cộng vecto (hình bình hành)
Ta có: U12 = 2U1O.cos(π/6) = U1O.√3
Vậy Ud = √3Up