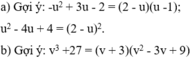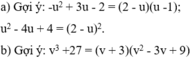
a)...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. \(1.\) \(a,\left(a+b\right)^2=a^2+2ab+b^2\) \(\left(a-b\right)^2+4ab=a^2-2ab+b^2+4ab=a^2+2ab+b^2\) \(\Rightarrow\left(a+b\right)^2=\left(a-b\right)^2+4ab\left(đpcm\right)\) a) \(x^2+x+1=x^2+x+\frac{1}{4}+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}>0\)(luôn dương) b) \(x^2-x+\frac{1}{2}=x^2-x+\frac{1}{4}+\frac{1}{4}=\left(x-\frac{1}{2}\right)^2+\frac{1}{4}>0\)(luôn dương) Tại vì nó được đề bài cho nên có nghĩa,k có nghĩa thì lm kiểu đếch j? Câu 2: a) \(ĐKXĐ:x\ne1\) \(A=\left(\frac{1}{x-1}-\frac{2x}{x^3+x-x^2-1}\right)\div\left(1-\frac{2x}{x^2+1}\right)\) \(\Leftrightarrow A=\left(\frac{1}{x-1}-\frac{2x}{\left(x-1\right)\left(x^2+1\right)}\right)\div\frac{x^2-2x+1}{x^2+1}\) \(\Leftrightarrow A=\frac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\div\frac{\left(x-1\right)^2}{x^2+1}\) \(\Leftrightarrow A=\frac{\left(x-1\right)^2\left(x^2+1\right)}{\left(x-1\right)\left(x^2+1\right)\left(x-1\right)^2}\) \(\Leftrightarrow A=\frac{1}{x-1}\) b) Để A > 0 \(\Leftrightarrow x-1>0\)(Vì\(1>0\)) \(\Leftrightarrow x>1\) Answer: Câu 1: \(\left(5x-x-\frac{1}{2}\right)2x\) \(=\left(4x-\frac{1}{2}\right)2x\) \(=4x.2x-\frac{1}{2}.2x\) \(=8x^2-x\) \(\left(x^3+4x^2+3x+12\right)\left(x+4\right)\) \(=x\left(x^3+4x^2+3x+12\right)+4\left(x^3+4x^2+3x+12\right)\) \(=x^4+4x^3+3x^2+12x+4x^3+16x^2+12x+48\) \(=x^4+\left(4x^3+4x^3\right)+\left(3x^2+16x^2\right)+\left(12x+12x\right)+48\) \(=x^4+8x^3+19x^2+24x+48\) Ta thay \(x=99\) vào phân thức \(\frac{x^2+1}{x-1}\): \(\frac{\left(99\right)^2+1}{99-1}=\frac{9802}{98}=\frac{4901}{49}\) Ta thay \(x=4\) vào phân thức \(\frac{x^2-x}{2\left(x-1\right)}\) : \(\frac{4^2-4}{2.\left(4-1\right)}=\frac{12}{6}=2\) \(\left(x+y\right)^2-\left(x-y\right)^2\) \(= (x²+2xy+y²)-(x²-2xy+y²)\) \(= x²+2xy+y²-x²+2xy-y²\) \(= 4xy\) \(4x^2+4x+1=\left(2x+1\right)^2=\left(2.2+1\right)^2=25\) Câu 2: \(x^2+x=0\) \(\Rightarrow x\left(x+1\right)=0\) \(\Rightarrow\orbr{\begin{cases}x=0\\x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=-1\end{cases}}\) \(x^2.\left(x-1\right)+4-4x=0\) \(\Rightarrow x^2.\left(x-1\right)+4\left(1-x\right)=0\) \(\Rightarrow\left(x-1\right)\left(x^2-4\right)=0\) \(\Rightarrow\left(x-1\right)\left(x-2\right)\left(x+2\right)=0\) Trường hợp 1: \(x-1=0\Rightarrow x=1\) Trường hợp 2: \(x-2=0\Rightarrow x=2\) Trường hợp 3: \(x+2=0\Rightarrow x=-2\) Câu 3: Bạn xem lại đề bài nhé. 1. Xét hiệu: \(x^3+y^3-\left(x^2y+xy^2\right)=\left(x^3-x^2y\right)-\left(xy^2+y^3\right)\) \(=x^2\left(x-y\right)-y^2\left(x-y\right)=\left(x-y\right)\left(x^2-y^2\right)\) \(=\left(x-y\right)\left(x-y\right)\left(x+y\right)=\left(x-y\right)^2\left(x+y\right)\ge0\), Với mọi x, y không âm Vậy \(x^3+y^3\ge x^2y+xy^2\)với mọi x, y không âm 2. \(111\left(x-2\right)\ge1998\Leftrightarrow x-2\ge\frac{1998}{11}\Leftrightarrow x\ge\frac{1998}{11}+2=\frac{2020}{11}\) 3. Xét hiệu: \(\frac{a-b}{b}-1=\frac{a}{b}-1-1=\frac{a}{b}-2>\frac{2b}{b}-2=2-2=0\)Với mọi , a, b dương Vậy \(\frac{a-b}{b}>1\)với mọi a, b dương 4) xét hiệu: \(x^2+y^2+z^2+14-\left(4x+2y+6z\right)\ge0\)\ <=> \(x^2-4x+4+y^2-2y+1+z^2-6z+9=\left(x-2\right)^2+\left(y-1\right)^2+\left(z-3\right)^2\ge0\)luôn đúng vs mọi x, y, z Vậy suy ra điều cần chứng minh 2, \(\frac{x^2}{2}+\frac{y^2}{3}+\frac{z^2}{4}=\frac{x^2+y^2+z^2}{5}\) <=>\(\left(\frac{x^2}{2}-\frac{x^2}{5}\right)+\left(\frac{y^2}{3}-\frac{y^2}{5}\right)+\left(\frac{z^2}{4}-\frac{z^2}{5}\right)=0\) <=>\(\frac{3}{10}x^2+\frac{2}{15}y^2+\frac{1}{20}z^2=0\) <=>x=y=z=0 4, a, \(\frac{1}{x\left(x^2+1\right)}=\frac{a}{x}+\frac{bx+c}{x^2+1}\) =>\(\frac{1}{x\left(x^2+1\right)}=\frac{ax^2+a+bx^2+cx}{x\left(x^2+1\right)}=\frac{\left(a+b\right)x^2+cx+a}{x\left(x^2+1\right)}\) Đồng nhất 2 phân thức ta được: \(\hept{\begin{cases}a+b=0\\c=0\\a=1\end{cases}\Leftrightarrow\hept{\begin{cases}b=-1\\c=0\\a=1\end{cases}}}\) b,a=1/4,b=-1/4 c, a=-1,b=1,c=1
K
Khách
CM
Cao Minh Tâm
26 tháng 2 2018
Đúng(0)
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 8 2019
2T
10 tháng 8 2019
22 tháng 11 2018
MN
7 tháng 3 2020
YN
21 tháng 12 2021
1 tháng 4 2019
1 tháng 4 2019
S
24 tháng 11 2018
S
24 tháng 11 2018
