Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
g'(x) là đạo hàm của g(x) phải không bạn? Xét đạo hàm tới 2 lần lận à?
VD1 : tanx≤4xπ∀x∈[0;π4]tanx≤4xπ∀x∈[0;π4]
Xét f(x)=tanx−4xπf(x)=tanx−4xπ
f′(x)=tan2x+1−4πf′(x)=tan2x+1−4π
f′′(x)=2tanx.1cos2x>0∀x∈[0;π4]f″(x)=2tanx.1cos2x>0∀x∈[0;π4]
Suy ra pt f′(x)=0f′(x)=0 có không quá 1 nghiệm thuộc [0;π4][0;π4]
Do đó f(x) đạt giá trị lớn nhất tại cực biên là khi x=0x=0 hoặc x=π4x=π4.
thay vào ta có max[0;π/4]f(x)=0max[0;π/4]f(x)=0
f(x)≤0⇔tanx≤4xπ∀x∈[0;π4]
a) ta có 2√5= = √20 ; 3√2 =
= √ 18 => 2√5 > 3√2
=> <
b) 6√3 = = √108 ; 3√6 =
= √54 => 6√3 > 3√6 =>
>
a) \(2\sqrt{5}=\sqrt{2^2.5}=\sqrt{20}\)
\(3\sqrt{2}=\sqrt{3^2.2}=\sqrt{18}\)
=> \(2\sqrt{5}>3\sqrt{2}\)
=> \(\left(\dfrac{1}{3}\right)^{2\sqrt{5}}< \left(\dfrac{1}{3}\right)^{3\sqrt{2}}\)
(vì cơ số \(\dfrac{1}{3}< 1\))
b) Vì \(3< 6^2\)
=> \(3^{\dfrac{1}{6}}< \left(6^2\right)^{\dfrac{1}{6}}\)
=> \(\sqrt[6]{3}< 6^{\dfrac{1}{3}}\)
=> \(\sqrt[6]{3}< \sqrt[3]{6}\)
=> \(7^{\sqrt[6]{3}}< 7^{\sqrt[3]{6}}\)
Lời giải:
BPT cần chứng minh tương đương \(2\sin x+\tan x-3x>0\)
Xét hàm \(f(x)=2\sin x+\tan x-3x\rightarrow f'(x)=2\cos x+\frac{1}{\cos^2 x}-3\)
Đặt \(\cos x=t\Rightarrow t\in (0;1)\)
Ta có \(f'(x)=2t+\frac{1}{t^2}-3=\frac{(t-1)(2t^2-t-1)}{t^2}>0\forall t\in (0;1)\)
Do đó \(f(x)\) luôn đồng biến với mọi \(x\in \left (0;\frac{\pi}{2}\right)\)
\(\Rightarrow f(x)>f(0)=0\). Ta có đpcm.
Lời giải:
Đặt \(\log_yx=a,\log_xy=b\). Khi đó ta có:
\(\left\{\begin{matrix} a+b=\frac{10}{3}\\ ab=\log_xy.\log_yx=1\end{matrix}\right.\)
Áp dụng định lý Viete đảo thì \(a,b\) là nghiệm của PT:
\(x^2-\frac{10}{3}x+1=0\) . PT trên có hai nghiệm \(3,\frac{1}{3}\)
Giả sử \(a=\log_yx=3\) và \(b=\log_xy=\frac{1}{3}\)
\(\left\{\begin{matrix} \log_y\left(\frac{144}{y}\right)=3\\ \log_x\left(\frac{144}{x}\right)=\frac{1}{3} \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=24\sqrt{3}\\ y=2\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow \frac{x+y}{2}=13\sqrt{3}\). Đáp án D
a) Xét hàm số y = f(x) = tanx – x với x ∈ [0 ;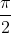
).
Ta có : y’ =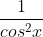
- 1 ≥ 0, x ∈ [0 ; 
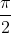); y’ = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ; 
).
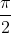Từ đó ∀x ∈ (0 ;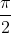
) thì f(x) > f(0) ⇔ tanx – x > tan0 – 0 = 0 hay tanx > x.
b) Xét hàm số y = g(x) = tanx – x -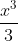
. với x ∈ [0 ; 
).
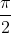Ta có : y’ =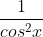
- 1 - x2 = 1 + tan2x - 1 - x2 = tan2x - x2
= (tanx - x)(tanx + x), ∀x ∈ [0 ;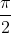
).
Vì ∀x ∈ [0 ;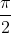
) nên tanx + x ≥ 0 và tanx - x >0 (theo câu a).
Do đó y' ≥ 0, ∀x ∈ [0 ;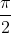
).
Dễ thấy y' = 0 ⇔ x = 0. Vậy hàm số luôn đồng biến trên [0 ;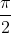
). Từ đó : ∀x ∈ [0 ; 
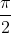) thì g(x) > g(0) ⇔ tanx – x - 
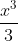> tan0 - 0 - 0 = 0 hay tanx > x + 
.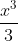