LT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TP
5 tháng 8 2017
b)
\(\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{2}{x.\left(x+1\right)}=\frac{2007}{2009}\)
\(=\frac{1}{1.3}+\frac{1}{2.3}+\frac{1}{2.5}+...+\frac{2}{x.\left(x+1\right)}=\frac{2007}{2009}\)
\(=\frac{1}{2}.\left(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{x.\left(x+1\right)}\right)=\frac{2007}{2009}\)
\(=\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{x}-\frac{1}{x+1}\right)=\frac{2007}{2009}:\frac{1}{2}\)
\(=\frac{1}{2}-\frac{1}{x+1}=\frac{2007}{4018}\)
\(=\frac{1}{x-1}=\frac{1}{2009}\Leftrightarrow x+1=2009\)
\(\Rightarrow x=2009-1=2008\)
6 tháng 8 2017
Bạn Phúc Trần Tấn bạn có biết làm phần a ko?Giúp mk với ạ!Mai mk cần rùi
3 tháng 9 2017
a>
\(\frac{1}{2^2}+\frac{1}{100^2}\)=1/4+1/10000
ta có 1/4<1/2(vì 2 đề bài muốn chứng minh tổng đó nhỏ 1 thì chúng ta phải xét xem có bao nhiêu lũy thừa hoặc sht thì ta sẽ lấy 1 : cho số số hạng )
1/100^2<1/2
=>A<1
1 tháng 4 2019
\(A=\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+...+\frac{1}{\left(2n\right)^2}< \frac{1}{2.4}+\frac{1}{4.6}+...+\frac{1}{\left(2n-2\right).2n}\)
\(< \frac{1}{2}\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+...+\frac{1}{2n-2}-\frac{1}{2n}\right)\)
\(< \frac{1}{2}.\left(\frac{1}{2}-\frac{1}{2n}\right)=\frac{1}{4}-\frac{1}{4n}< \frac{1}{4}\)
\(\Rightarrow\) \(A< \frac{1}{4}\)
Study well ! >_<
VC
Vũ Cao Minh⁀ᶦᵈᵒᶫ ( ✎﹏IDΣΛ亗 )
CTV
VIP
24 tháng 6 2020
Đặt \(A=\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{2140.2141}\)
Có \(\frac{1}{2^3}< \frac{1}{2.3};\frac{1}{3^3}< \frac{1}{3.4};...;\frac{1}{2140^3}< \frac{1}{2140.2141}\)
\(\Rightarrow\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}+...+\frac{1}{2140^3}< A\). Từ đó ta tính được A
\(A=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{2140}-\frac{1}{2141}\)
\(A=\frac{1}{2}-\frac{1}{2141}\Rightarrow A>\frac{1}{2}\). Mà \(\frac{1}{2}< \frac{2}{3}\Rightarrow A< \frac{2}{3}\)
Có \(\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}+...+\frac{1}{2140^3}< A\Rightarrow\)\(\frac{1}{2^3}+\frac{1}{3^3}+\frac{1}{4^3}+...+\frac{1}{2140^3}< \frac{2}{3}\)
11 tháng 4 2018
Ta có \(\frac{1}{3^2}< \frac{1}{2\cdot3}\)
\(\frac{1}{4^2}< \frac{1}{3\cdot4}\)
.....................
\(\frac{1}{100^2}< \frac{1}{99\cdot100}\)
\(\Rightarrow\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< \frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{99\cdot100}\)
\(\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< \frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(\Rightarrow\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< \frac{1}{2}-\frac{1}{100}< \frac{1}{2}\)
Vậy \(\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< \frac{1}{2}\)
TV
11 tháng 4 2018
1/3^2 + 1/4^2 + 1/5^2 + 1/6^2 + ... + 1/100^2 < 1/2
1/3.3 + 1/4.4 + 1/5.5 + 1/6.6 + ... + 1/100.100 < 1/2.3+ 1/3.4 + 1/4 .5 + 1/5.6 + .. + 1/99.100
1/3.3 + 1/4.4 + 1/5.5 + 1/6.6 + ... + 1/100.100 < 1/2 - 1/3 + 1/3 - 1/4 + 1/4 - 1/5 + 1/5 - 1/6 + ... + 1/99 - 1/100
1/3.3 + 1/4.4 + 1/5.5 + 1/6.6 + ... + 1/100.100 < 1/2 - 1/100 suy ra 1/3^2 + 1/4^2 + 1/5^2 + 1/6^2 + ... + 1/100^2 < 1/2
Chúc bn hok tốt
NA
1
S
14 tháng 5 2017
\(A=\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+...+\frac{1}{100^2}\)
\(2^2A=\frac{2^2}{4^2}+\frac{2^2}{6^2}+\frac{2^2}{8^2}+...+\frac{2^2}{100^2}\)
\(4A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{50^2}\)
Ta có: \(\frac{1}{2^2}< \frac{1}{1.2};\frac{1}{3^2}< \frac{1}{2.3};\frac{1}{4^2}< \frac{1}{3.4};.....;\frac{1}{50^2}< \frac{1}{49.50}\)
\(\Rightarrow4A< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{49.50}\)
=> \(4A< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{49}-\frac{1}{50}\)
=>\(4A< 1-\frac{1}{50}\)
=> 4A < 1
=> A < \(\frac{1}{4}\)(đpcm)
11 tháng 4 2020
a)Ta có: 22>1.2⇒\(\frac{1}{2^2}< \frac{1}{1.2}\)
32>2.3⇒\(\frac{1}{3^2}< \frac{1}{2.3}\)
... 1002>99.100 ⇒ \(\frac{1}{100^2}< \frac{1}{99.100}\)
VT < \(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}\)\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}\)\(=1-\frac{1}{100}< 1\)(ĐPCM)
27 tháng 3 2019
a)\(\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{10^2}< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{9.10}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{9}-\frac{1}{10}\)
\(=1-\frac{1}{10}< 1\)
Vậy \(A< 1\)
DT
27 tháng 3 2019
a) ta có: \(\frac{1}{2^2}\)<\(\frac{1}{1.2}\);\(\frac{1}{3^2}\)<\(\frac{1}{2.3}\)....\(\frac{1}{10^2}\)<\(\frac{1}{9.10}\)
Đặt A=\(\frac{1}{2^2}\)+\(\frac{1}{3^2}\)+...+\(\frac{1}{10^2}\)<\(\frac{1}{1.2}\)+\(\frac{1}{2.3}\)+....+\(\frac{1}{9.10}\)
\(\Rightarrow\)A<1-\(\frac{1}{2}\)+\(\frac{1}{2}\)-\(\frac{1}{3}\)+...+\(\frac{1}{9}\)-\(\frac{1}{10}\)
\(\Rightarrow\)A<1-\(\frac{1}{10}\)
\(\Rightarrow\)A<1
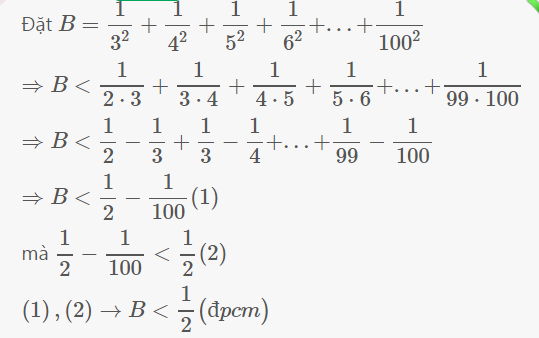
\(\frac{1}{2^2}+\frac{1}{4^2}+\frac{1}{6^2}+\frac{1}{8^2}+...+\frac{1}{100^2}\)
\(=\frac{1}{2^2}\left(1+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}\right)\)
Đặt \(A=\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}\)
Ta có: \(\frac{1}{2^2}< \frac{1}{1\cdot2};\frac{1}{3^2}< \frac{1}{2\cdot3};....;\frac{1}{50^2}< \frac{1}{49\cdot50}\)
\(\Rightarrow A< \frac{1}{1\cdot2}+\frac{1}{2\cdot3}+....+\frac{1}{49\cdot50}\)
\(\Rightarrow A< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{49}-\frac{1}{50}\)
\(\Rightarrow A< 1-\frac{1}{50}\)
\(\Rightarrow A< 1\Rightarrow1+A< 1+1=2\)
\(\Rightarrow\frac{1}{2^2}\cdot\left(1+A\right)< \frac{1}{2^2}\cdot2=\frac{1}{2}\)(đpcm)