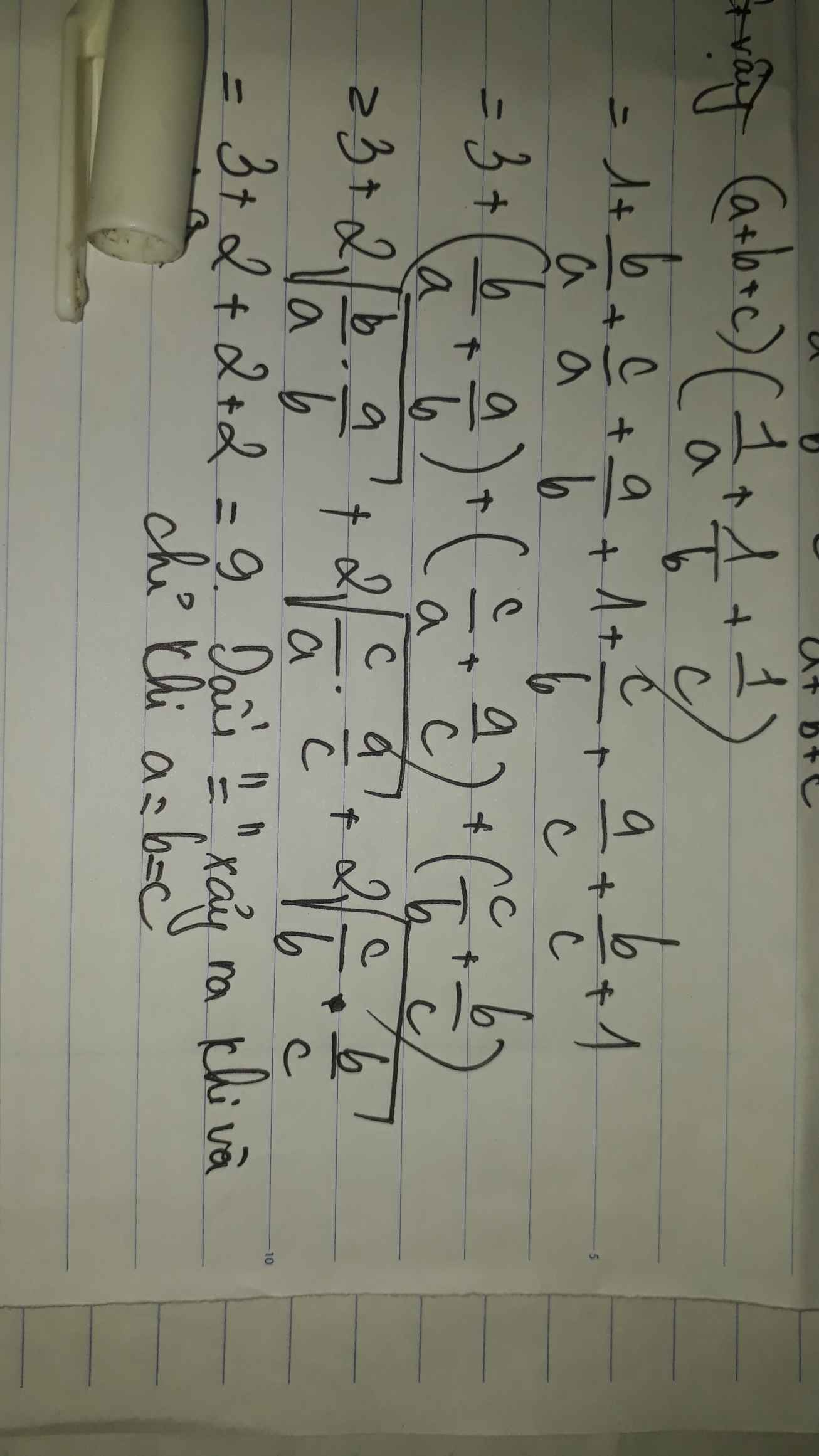K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
0
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2019
\(\Leftrightarrow\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\left(a+b+c\right)\ge9\)
Theo BĐT Cauchy ta có:
\(\left\{{}\begin{matrix}\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{3}{\sqrt[3]{abc}}\\a+b+c\ge3\sqrt[3]{abc}\end{matrix}\right.\)
\(\Rightarrow\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\left(a+b+c\right)\ge\frac{3}{\sqrt[3]{abc}}.3\sqrt[3]{abc}=9\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
KT
10 tháng 5 2018
mình bổ sung thêm đề: a,b dương
BÀI LÀM
\(\left(1+\frac{1}{a}\right)\left(1+\frac{1}{b}\right)\)
\(=\left(1+\frac{a+b}{a}\right)\left(1+\frac{a+b}{b}\right)\) (thay a+b = 1)
\(=\left(1+\frac{a}{a}+\frac{b}{a}\right)\left(1+\frac{a}{b}+\frac{b}{b}\right)\)
\(=\left(2+\frac{b}{a}\right)\left(2+\frac{a}{b}\right)\)
\(=4+2\left(\frac{a}{b}+\frac{b}{a}\right)+\frac{b}{a}.\frac{a}{b}\)
\(=5+2\left(\frac{a}{b}+\frac{b}{a}\right)\) \(\ge5+2.2=9\) (1)
c/m: \(\frac{a}{b}+\frac{b}{a}\ge2\) với a,b dương
\(\Leftrightarrow\) \(\frac{a^2}{ab}+\frac{b^2}{ab}\ge\frac{2ab}{ab}\)
\(\Leftrightarrow\)\(\frac{a^2}{ab}+\frac{b^2}{ab}-\frac{2ab}{ab}\ge0\)
\(\Leftrightarrow\)\(\frac{\left(a-b\right)^2}{ab}\ge0\) luôn đúng
Dấu "=" xảy ra \(\Leftrightarrow\)\(a=b\)
Vậy BĐT (1) đã được chứng minh
Dấu "=" xảy ra \(\Leftrightarrow\)\(a=b=\frac{1}{2}\)
KR
10 tháng 5 2018
Theo Cauchy , ta có \(a+b\ge2\sqrt{ab}\Rightarrow\sqrt{ab}\le\frac{a+b}{2}\)
Áp dụng bất đẳng thức Bunyakovsky , ta có :
\(\left(1+\frac{1}{a}\right)\left(1+\frac{1}{b}\right)\ge\left(1+\frac{1}{\sqrt{a}.\sqrt{b}}\right)^2\ge\left(1+\frac{1}{\frac{\left(a+b\right)}{2}}\right)^2=\left(1+2\right)^2=9\)
Đẳng thức xảy ra <=> a = b = 1/2
1 tháng 4 2023
a: \(\dfrac{a}{b}+\dfrac{b}{a}>=2\cdot\sqrt{\dfrac{a}{b}\cdot\dfrac{b}{a}}=2\)
b: a<b
=>-2a>-2b
=>-2a-3>-2b-3
c: =x^2+2xy+y^2+y^2+6y+9
=(x+y)^2+(y+3)^2>=0 với mọi x,y
d: a+3>b+3
=>a>b
=>-5a<-5b
=>-5a+1<-5b+1
PN
5 tháng 7 2020
Áp dụng bđt Cauchy cho 2 số không âm :
\(x^2+\frac{1}{x}\ge2\sqrt[2]{\frac{x^2}{x}}=2.\sqrt{x}\)
\(y^2+\frac{1}{y}\ge2\sqrt[2]{\frac{y^2}{y}}=2.\sqrt{y}\)
Cộng vế với vế ta được :
\(x^2+y^2+\frac{1}{x}+\frac{1}{y}\ge2.\sqrt{x}+2.\sqrt{y}=2\left(\sqrt{x}+\sqrt{y}\right)\)
Vậy ta có điều phải chứng mình
5 tháng 7 2020
Ta đi chứng minh:\(a^3+b^3\ge ab\left(a+b\right)\)
\(\Leftrightarrow\left(a-b\right)^2\left(a+b\right)\ge0\)* đúng *
Khi đó:
\(\frac{1}{a^3+b^3+abc}\le\frac{1}{ab\left(a+b\right)+abc}=\frac{1}{ab\left(a+b+c\right)}=\frac{c}{abc\left(a+b+c\right)}\)
Tương tự:
\(\frac{1}{b^3+c^3+abc}\le\frac{a}{abc\left(a+b+c\right)};\frac{1}{c^3+a^3+abc}\le\frac{b}{abc\left(a+b+c\right)}\)
\(\Rightarrow LHS\le\frac{a+b+c}{abc\left(a+b+c\right)}=\frac{1}{abc}\)
NT
1
27 tháng 4 2018
\(\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)\ge9\)
\(\Leftrightarrow1+\dfrac{1}{b}+\dfrac{1}{a}+\dfrac{1}{ab}\ge9\)
Lại có:\(\dfrac{1}{b}+\dfrac{1}{a}\ge\dfrac{4}{a+b}=4\)
\(ab\le\dfrac{\left(a+b\right)^2}{4}=\dfrac{1}{4}\)\(\Rightarrow\dfrac{1}{ab}\ge\dfrac{1}{\dfrac{1}{4}}=4\)
\(\Rightarrow1+\dfrac{1}{b}+\dfrac{1}{a}+\dfrac{1}{ab}\ge1+4+4=9\left(\text{đ}pcm\right)\)
TL
1
15 tháng 5 2022
áp dụng bất đẳng thức AM-GM ta có:
1/a+1/b+1/c>=9/(a+b+c)
=> 1/a+1/b+1/c>=9/1
=> 1/a+1/b+1/c>=9