Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Đúng vì vectơ \(\overrightarrow 0 \) cùng hướng với mọi vectơ.
b) Sai. Chẳng hạn: Hai vecto không cùng hướng nhưng cũng không ngược hướng (do chúng không cùng phương).

c) Đúng.
\(\overrightarrow a \) và \(\overrightarrow b \) đều cùng phương với \(\overrightarrow c \) thì a // c và b // c do đó a // b tức là \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương.
d) Đúng.
\(\overrightarrow a \) và \(\overrightarrow b \) đều cùng hướng với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương , cùng chiều đo đó cùng hướng.

Chọn D. Đây là một tính chất của tích vô hướng.
A. Sai vì \(({\overrightarrow a .\overrightarrow b})\overrightarrow c = [ {|\overrightarrow a |.|\overrightarrow b |\;\,\cos ( {\overrightarrow a ,\overrightarrow b } )} ].\overrightarrow c \ne \)\(\overrightarrow a \,\,( {\overrightarrow b .\overrightarrow c }) = \overrightarrow a \,\,[ {|\overrightarrow b |.|\overrightarrow c |\;\,\cos ( {\overrightarrow b ,\overrightarrow c })}]\)
B. Sai vì \((\overrightarrow a .\overrightarrow b)^2 = {[{\overrightarrow a .\overrightarrow b = | {\overrightarrow a } |.| {\overrightarrow b }|\,\cos ( {\overrightarrow a ,\overrightarrow b })}]^2} = {\overrightarrow a ^2}\,.\,{\overrightarrow b ^2}.{\cos ^2}( {\overrightarrow a ,\overrightarrow b } )\)\( \ne \;\;{\overrightarrow a ^2}\,.\,{\overrightarrow b ^2}\)
C. Sai vì \(\overrightarrow a .\overrightarrow b = | {\overrightarrow a }|.| {\overrightarrow b } |\,\cos ( {\overrightarrow a ,\overrightarrow b }) \ne | {\overrightarrow a }|.| {\overrightarrow b }|\,\sin ( {\overrightarrow a ,\overrightarrow b })\)

Tham khảo:
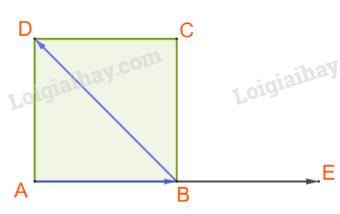
A. Ta có: \(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = \left( {\overrightarrow {BE} ,\overrightarrow {BD} } \right) = {135^o} \ne {45^o}.\) Vậy A sai.
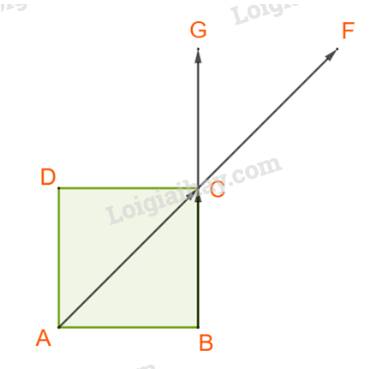
B. Ta có: \(\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {CF} ,\overrightarrow {CG} } \right) = {45^o}\) và \(\overrightarrow {AC} .\overrightarrow {BC} = AC.BC.\cos {45^o} = a\sqrt 2 .a.\frac{{\sqrt 2 }}{2} = {a^2}.\)
Vậy B đúng.
Chọn B
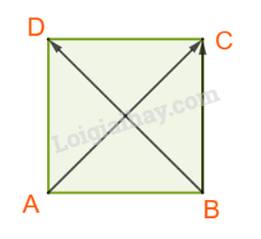
C. Dễ thấy \(AC \bot BD\) nên \(\overrightarrow {AC} .\overrightarrow {BD} = 0 \ne {a^2}\sqrt 2.\) Vậy C sai.
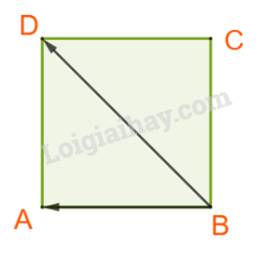
D. Ta có: \(\left( {\overrightarrow {BA} .\overrightarrow {BD} } \right) = {45^o}\) \( \Rightarrow \overrightarrow {BA} .\overrightarrow {BD} = BA.BD.\cos {45^o} = a.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = {a^2} \ne - {a^2}.\) Vậy D sai.

a)
+) Vectơ \(\overrightarrow a \) cùng phương với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow a \) song song với giá của vectơ \(\overrightarrow c \)
+) Vectơ \(\overrightarrow b \) cùng phương với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow b \) song song với giá của vectơ \(\overrightarrow c \)
Suy ra giá của vectơ \(\overrightarrow a \) và vectơ \(\overrightarrow b \) song song với nhau nên \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Vậy khẳng định trên đúng
b) Giả sử vectơ \(\overrightarrow c \) có hướng từ A sang B
+) Vectơ \(\overrightarrow a \) ngược hướng với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow a \) song song với giá của vectơ \(\overrightarrow c \) và có hướng từ B sang A
+) Vectơ \(\overrightarrow b \) ngược hướng với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow b \) song song với giá của vectơ \(\overrightarrow c \) và có hướng từ B sang A
Suy ra, hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng
Vậy khẳng định trên đúng

4 là khẳng định đúng, \(\overrightarrow{i}=\left(1;0\right);\overrightarrow{j}=\left(0;1\right)\)

Khẳng định trên sai. Vì khi 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương nhưng chưa chắc là cùng hướng.
Chẳng hạn:
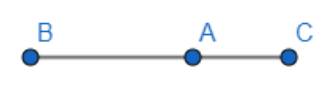
Khi A nằm giữa B và C thì hướng của vectơ \(\overrightarrow {AB} \) là từ phải sang trái, còn hướng của vectơ \(\overrightarrow {AC} \)là từ trái sang phải nên hai vectơ này là ngược hướng.

a) Hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \) có cùng độ dài bằng \(\left| {kt} \right|.\left| {\overrightarrow u } \right|\)
Ta có: \(\left| {t\overrightarrow u } \right| = \left| t \right|\left| {\overrightarrow u } \right| \Rightarrow \left| {k\left( {t\overrightarrow u } \right)} \right| = \left| k \right|\left| {\left( {t\overrightarrow u } \right)} \right| = \left| k \right|.\left| t \right|\left| {\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)
Và \(\left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)
\( \Rightarrow \left| {k\left( {t\overrightarrow u } \right)} \right| = \left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)
b) Nếu \(kt \ge 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)
Ta xét 2 trường hợp:
Trường hợp 1: \(k \ge 0,t \ge 0\)
Vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(t\overrightarrow u \) (vì \(k \ge 0\) ), mà vecto \(t\overrightarrow u \) cùng hướng với vecto \(\overrightarrow u \) (vì \(t \ge 0\) )
Do đó vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(\overrightarrow u \).
Trường hợp 2: \(k < 0,t < 0\)
Vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(t\overrightarrow u \) (vì \(k < 0\) ), mà vecto \(t\overrightarrow u \) ngược hướng với vecto \(\overrightarrow u \) (vì \(t < 0\) )
Do đó vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(\overrightarrow u \).
Vậy vecto \(k\left( {t\overrightarrow u } \right)\) luôn cùng hướng với vecto \(\overrightarrow u \) nếu \(kt \ge 0\).
Lại có: \(kt \ge 0\) nên \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)
Vậy \(kt \ge 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)
c) Nếu \(kt < 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)
Ta xét 2 trường hợp:
Trường hợp 1: \(k > 0,t < 0\)
Vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(t\overrightarrow u \) (vì \(k > 0\) ), mà vecto \(t\overrightarrow u \) ngược hướng với vecto \(\overrightarrow u \) (vì \(t < 0\))
Do đó vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(\overrightarrow u \).
Trường hợp 2: \(k < 0,t > 0\)
Vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(t\overrightarrow u \) (vì \(k < 0\) ), mà vecto \(t\overrightarrow u \) cùng hướng với vecto \(\overrightarrow u \) (vì \(t > 0\))
Do đó vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(\overrightarrow u \).
Vậy vecto \(k\left( {t\overrightarrow u } \right)\) luôn ngược hướng với vecto \(\overrightarrow u \) nếu \(kt < 0\).
Lại có: \(kt < 0\) nên \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)
Vậy \(kt < 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)
d)
Từ ý b) và c), ra suy ra hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \)luôn cùng hướng.
Theo câu a) ta có: \(\left| {k\left( {t\overrightarrow u } \right)} \right| = \left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)
\( \Rightarrow \) Hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \) bằng nhau
Đề thiếu. Bạn xem lại đề.