Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\Delta OAB.cân.tại.O\left(OA=OB=R\right)\) nên OH là trung tuyến cũng là đường cao \(\Rightarrow OH\perp AB\left(1\right)\)
\(\Delta OCD.cân.tại.O\left(OC=OD=R\right)\) nên Ok là trung tuyến cũng là đường cao \(\Rightarrow OK\perp CD\left(2\right)\)
Ta có \(AB//CD\left(gt\right)\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow OH.trùng.OK\Rightarrow O;H;K\) thẳng hàng
\(b,AH=\dfrac{1}{2}AB=8\left(cm\right);OA=R=10\left(cm\right)\\ \Rightarrow OH=\sqrt{OA^2-AH^2}=6\left(cm\right)\left(pytago\right)\\ \Rightarrow OK=HK-OH=14-6=8\left(cm\right)\\ Mà.OC=R=10\left(cm\right)\\ \Rightarrow CK=\sqrt{OC^2-OK^2}=6\left(cm\right)\\ Mà.CK=\dfrac{1}{2}CD\\ \Rightarrow CD=12\left(cm\right)\)

a: Ta có: OH\(\perp\)AB
mà AB//CD
nên OH\(\perp\)CD
mà OK\(\perp\)CD
và OH,OK có điểm chung là O
nên H,O,K thẳng hàng

a: Ta có: OH\(\perp\)AB
mà AB//CD
nên OH\(\perp\)CD
mà OK\(\perp\)CD
và OH,OK có điểm chung là O
nên H,O,K thẳng hàng

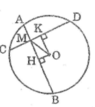
Ta có: HA = HB (gt)
Suy ra : OH ⊥ AB (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : OK ⊥ CD (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
O M 2 = O H 2 + H M 2
Suy ra : H M 2 = O M 2 - O H 2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
O M 2 = O K 2 + K M 2
Suy ra: K M 2 = O M 2 - O K 2 (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: H M 2 > K M 2 hay HM > KM