
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

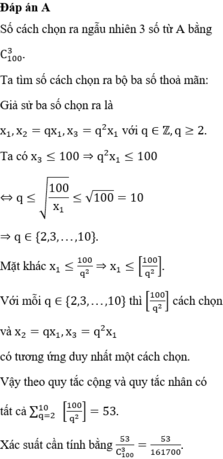

Câu 1 : Việc gõ ký hiệu như bạn đề cập ; mình cũng không biết phải làm sao nên cứ dùng xyz vậy thôi.
Ta có:
xyz = 100x +10y +z = 111x -11x +10y +z = 37.3x -(11x-10y-z) chia hết cho 37
=> (11x-10y-z) chia hết cho 37
Lại có:
xyz -yzx = 100x +10y +z -100y -10z -x = 99x -90y -9z = 9.(11x-10y-z) chia hết cho 37
Vậy yzx cũng phải chia hết cho 37
Có thể phát biểu hay hơn là CMR: Khi hoán vị các chữ số của 1 số có 3 chữ số chia hết cho 37 thì được số mới cũng chia hết cho 37.

2.
Gọi quãng đường cần tìm là s.---> vận tốc Xuân= s/12,
--> vận tốc Hạ=s/10
thời gian Xuân gặp Hạ: 50/(s/12)= (s-50)/(s/10)
50x12/s= (s-50)x10/s
50x12=10s-500
---> s = (500+50x12)/10= 110
quãng đường giữa nhà hai bạn là 110m
4.
Khi ngược dòng 1 giờ ta đi được số phần quãng sông là:
1 : 8 = 1/8 (quãng sông)
Khi xuôi dòng 1 giờ ta đi được số phần quãng sông là:
1 : 4 = 1/4 (quãng sông)
Bèo trôi theo ta về 1 giờ trôi được số phần quãng sông là:
(1/4 - 1/8) : 2 = 1/16 (quãng sông)
Bèo trôi theo ta về cập bến sau số giờ là:
1 : 1/16 = 16 (giờ)
Đ/s: 16 giờ

Năm số được chọn ra xếp được duy nhất dãy tăng, giả sử là
x 1 < x 2 < x 3 < x 4 < x 5
Theo giả thiết các số đó là x 1 , q x 1 , q 2 x 1 , q 3 x 1 , q 4 x 1 và q ∈ ℕ , q ≥ 2
Vì ![]()
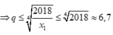
![]()
Mặt khác
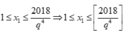
Vậy với mỗi số nguyên q thuộc tập X={ 2;3;4;5;6}
ta có 2018 q 4 cách chọn x1 các số x2, x3, x4, x5 có tương ứng duy nhất một cách chọn.
Vậy theo quy tắc cộng và quy tắc nhân có tất cả
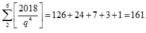
Chọn đáp án B.