Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Các loại đơn vị đo:
+ Đơn vị đo độ dài: m, km, cm, …
+ Đơn vị đo vận tốc, tốc độ: m/s, km/h, …
+ Đơn vị đo thời gian: giây, giờ, phút, …
+ Đơn vị đo lực: Niuton (N)
…
- Các loại sai số có thể gặp:
+ Sai số ngẫu nhiên
+ Sai số hệ thống
- Cách hạn chế các loại sai số:
+ Khắc phục sai số ngẫu nhiên: thực hiện nhiều lần đo, lấy giá trị trung bình để hạn chế sự phân tán của số liệu đo.
+ Khắc phục sai số hệ thống: thường xuyên hiệu chỉnh dụng cụ đo, sử dụng thiết bị đo có độ chính xác cao.

- Để xác định được các sai số này, chúng ta cần tính được các sai số hệ thống và sai số ngẫu nhiên, tính toán các sai số.
- Nguyên nhân gây ra sai số có thể do nguyên nhân khách quan (do dụng cụ, điều kiện thực hành, thời tiết, nhiệt độ, độ ẩm), nguyên nhân chủ quan (thao tác đo chưa chính xác) hoặc có thể do dụng cụ ban đầu đã có sai số (sai số hệ thống).
- Cách khắc phục: thao tác đúng cách, lựa chọn thiết bị phù hợp, tiến hành đo nhiều lần.

Sai số ngẫu nhiên được xác định như sau:
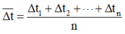
Trong đó:
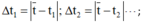
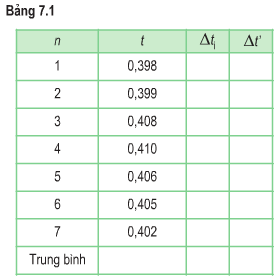
Sai số dụng cụ Δt’ thông thường có thể lấy bằng nửa hoặc một độ chia nhỏ nhất. Ở đây, qua giá trị trong bảng ta thấy phép đo thời gian có sai số dụng cụ với độ chia nhỏ nhất là 0,001s → Δt’ = 0,001s
Tính toán ta thu được bảng số liệu sau:
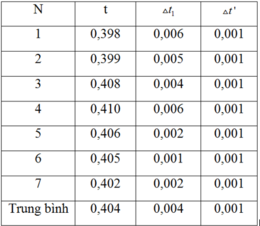


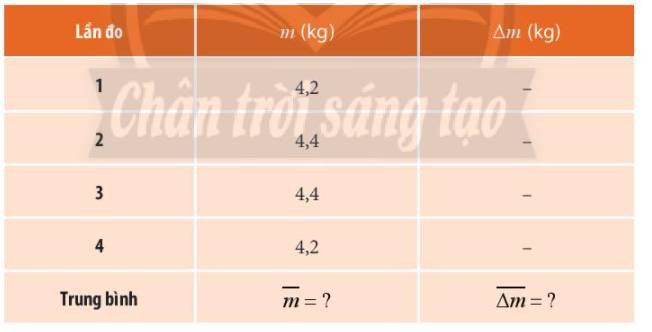
Giá trị trung bình khối lượng của túi trái cây là:
\(\overline m = \frac{{{m_1} + {m_2} + {m_3} + {m_4}}}{4} = \frac{{4,2 + 4,4 + 4,4 + 4,2}}{4} = 4,3(kg)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {m_1} = \left| {\overline m - {m_1}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\\\Delta {m_2} = \left| {\overline m - {m_2}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_3} = \left| {\overline m - {m_3}} \right| = \left| {4,3 - 4,4} \right| = 0,1(kg)\\\Delta {m_4} = \left| {\overline m - {m_4}} \right| = \left| {4,3 - 4,2} \right| = 0,1(kg)\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta m} = \frac{{\Delta {m_1} + \Delta {m_2} + \Delta {m_3} + \Delta {m_4}}}{4} = \frac{{0,1 + 0,1 + 0,1 + 0,1}}{4} = 0,1(kg)\)
Sai số tuyệt đối của phép đo là:
\(\Delta m = \overline {\Delta m} + \Delta {m_{dc}} = 0,1 + 0,1 = 0,2(kg)\)
Sai số tương đối của phép đo là:
\(\delta m = \frac{{\Delta m}}{{\overline m }}.100\% = \frac{{0,2}}{{4,2}}.100\% = 4,65\% \)
Kết quả phép đo:
\(m = \overline m \pm \Delta m = 4,3 \pm 0,2(kg)\)

|
n |
t |
∆ti |
∆t’ |
|
1 |
0,398 |
0,006 |
|
|
2 |
0,399 |
0,005 |
|
|
3 |
0,408 |
0,004 |
|
|
4 |
0,410 |
0,006 |
|
|
5 |
0,406 |
0,002 |
|
|
6 |
0,405 |
0,001 |
|
|
7 |
0,402 |
0,002 |
|
|
Trung bình |
0,404 |
0,004 |
0,001 |