Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: x-y-z=0
=>x=y+z; y=x-z; z=x-y
\(K=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}=\dfrac{y\cdot\left(-z\right)\cdot x}{xyz}=-1\)
b: Tham khảo:
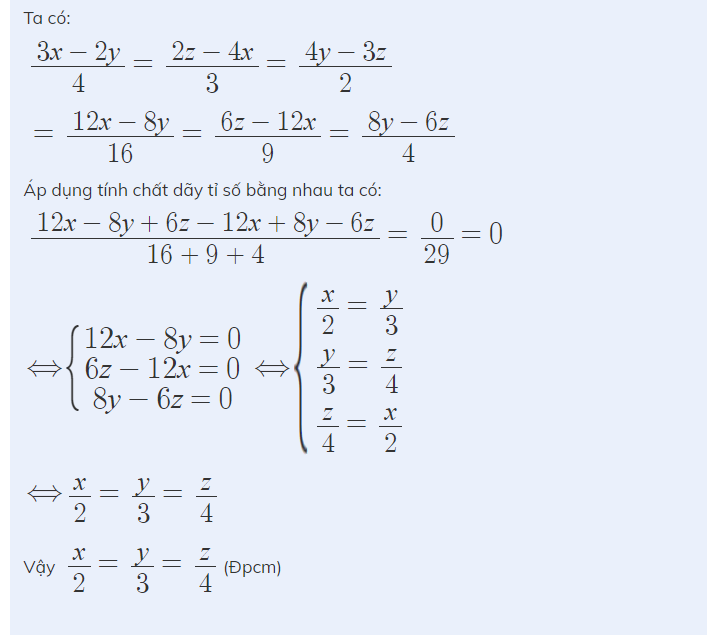

\(x^3+y^3+z^3=3xyz\)
\(x^3+y^3+z^3-3xyz=0\)
\(\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)=0\)
\(x^2+y^2+z^2-xy-xz-yz=0\left(x+y+z\ne0\right)\)
\(2\times\left(x^2+y^2+z^2-xy-xz-yz\right)=0\times2\)
\(2x^2+2y^2+2z^2-2xy-2xz-2yz=0\)
\(x^2-2xy+y^2+x^2-2xz+z^2+y^2-2yz+z^2=0\)
\(\left(x-y\right)^2+\left(x-z\right)^2+\left(y-z\right)^2=0\)
\(\left[\begin{array}{nghiempt}x-y=0\\x-z=0\\y-z=0\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=y\\x=z\\y=z\end{array}\right.\)
x = y = z
\(P=\left(1+\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\left(1+\frac{x}{z}\right)\)
\(=\left(1+\frac{x}{x}\right)\left(1+\frac{y}{y}\right)\left(1+\frac{z}{z}\right)\)
\(=\left(1+1\right)\left(1+1\right)\left(1+1\right)\)
\(=2^3\)
\(=8\)

dat a=x-y
b=y-z
c=z-x
a+b+c=0=x+y+z
\(\left(\frac{a}{z}+\frac{b}{x}+\frac{c}{y}\right)\left(\frac{z}{a}+\frac{x}{b}+\frac{y}{c}\right)\)
dung bumiakopsky de giai
...........................................

1)\(A=\frac{b\left(2a\left(a+5b\right)+\left(a+5b\right)\right)}{a-3b}.\frac{a\left(a-3b\right)}{ab\left(a+5b\right)}=\frac{b\left(a+5b\right)\left(2a+1\right).a\left(a-3b\right)}{\left(a-3b\right).ab\left(a+5b\right)}\)
\(A=2a+1\)=>lẻ với mọi a thuộc z=> dpcm
2) từ: x+y+z=1=> xy+z=xy+1-x-y=x(y-1)-(y-1)=(y-1)(x-1)
tường tự: ta có tử của Q=(x-1)^2.(y-1)^2.(z-1)^2=[(x-1)(y-1)(z-1)]^2=[-(z+y).-(x+y).-(x+y)]^2=Mẫu=> Q=1
3) kiểm tra lại xem đề đã chuẩn chưa

Từ \(\frac{x}{y-z}+\frac{y}{z-x}+\frac{z}{x-y}=0\Rightarrow\frac{x}{y-z}=-\frac{y}{z-x}-\frac{z}{x-y}\)
\(\Rightarrow\frac{x}{y-z}=\frac{y}{x-z}+\frac{z}{y-x}\)
\(\Leftrightarrow\frac{x}{y-z}=\frac{y\left(y-x\right)+z\left(x-z\right)}{\left(x-z\right)\left(y-x\right)}\)
\(\Leftrightarrow\frac{x}{y-z}=\frac{y^2-xy+zx-z^2}{\left(x-z\right)\left(y-x\right)}\)
\(\Leftrightarrow\frac{x}{\left(y-z\right)^2}=\frac{y^2-xy+zx-z^2}{\left(x-z\right)\left(y-x\right)\left(y-z\right)}\)
C/m tương tự đc \(\frac{y}{\left(z-x\right)^2}=\frac{z^2-yz+xy-x^2}{\left(x-z\right)\left(y-z\right)\left(y-z\right)}\)
\(\frac{z}{\left(x-y\right)^2}=\frac{x^2-xz+zy-y^2}{\left(x-z\right)\left(y-x\right)\left(y-z\right)}\)
Khi đó \(Q=\frac{y^2-xy+xz-z^2+z^2-yz+xy-x^2+x^2-xz+yz-y^2}{\left(x-z\right)\left(y-x\right)\left(y-z\right)}=0\)
Vậy Q=0
\(\frac{2}{3}x=\frac{3}{4}y=\frac{4}{5}z\)
\(\Leftrightarrow\)\(\frac{2x}{3}.\frac{1}{12}\)\(=\)\(\frac{3y}{4}.\frac{1}{12}\)\(=\)\(\frac{4z}{5}.\frac{1}{12}\)
\(\Leftrightarrow\)\(\frac{x}{18}=\frac{y}{16}=\frac{z}{15}\)
Ap dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{18}=\frac{y}{16}=\frac{z}{15}=\frac{x+y-z}{18+16-15}=\frac{38}{19}=2\)
suy ra: \(\hept{\begin{cases}\frac{x}{18}=2\\\frac{y}{16}=2\\\frac{z}{15}=2\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x=36\\y=32\\z=30\end{cases}}\)
Vậy \(x=36;\) \(y=32;\) \(z=30\)