HT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 4 2017
thi cấp tỉnh mà có bài là quá ngon rồi !
Áp dụng BĐT \((a+b+c)^2 \geq 3(ab+bc+ca)\) ta có:
\(\left(\dfrac{xy}{z}+\dfrac{xz}{y}+\dfrac{yz}{x}\right)^2 \geq 3(x^2+y^2+z^2)=9\)
\(\Leftrightarrow \dfrac{xy}{z}+\dfrac{xz}{y}+\dfrac{yz}{x} \geq 3\)
Đẳng thức xảy ra khi \(x=y=z=1\)
10 tháng 4 2018
Bạn ơi đây đâu phải toán lớp 9.
Cho gì vậy bạn.
Chứng minh cái gì .
Bạn đăng rõ câu hỏi đi chứ !!!
13 tháng 8 2017
3) Đặt b+c=x;c+a=y;a+b=z.
=>a=(y+z-x)/2 ; b=(x+z-y)/2 ; c=(x+y-z)/2
BĐT cần CM <=> \(\frac{y+z-x}{2x}+\frac{x+z-y}{2y}+\frac{x+y-z}{2z}\ge\frac{3}{2}\)
VT=\(\frac{1}{2}\left(\frac{y}{x}+\frac{z}{x}-1+\frac{x}{y}+\frac{z}{y}-1+\frac{x}{z}+\frac{y}{z}-1\right)\)
\(=\frac{1}{2}\left[\left(\frac{x}{y}+\frac{y}{x}\right)+\left(\frac{y}{z}+\frac{z}{y}\right)+\left(\frac{x}{z}+\frac{z}{x}\right)-3\right]\)
\(\ge\frac{1}{2}\left(2+2+2-3\right)=\frac{3}{2}\)(Cauchy)
Dấu''='' tự giải ra nhá
13 tháng 8 2017
Bài 4
dễ chứng minh \(\left(a+b\right)^2\ge4ab;\left(b+c\right)^2\ge4bc;\left(a+c\right)^2\ge4ac\)
\(\Rightarrow\left(a+b\right)^2\left(b+c\right)^2\left(a+c\right)^2\ge64a^2b^2c^2\)
rồi khai căn ra \(\Rightarrow\)dpcm.
đấu " = " xảy ra \(\Leftrightarrow\)\(a=b=c\)
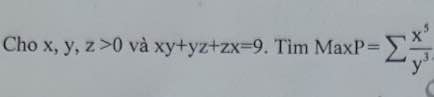
Nếu biểu thức là: \(P=\dfrac{x^5}{y^3}+\dfrac{y^5}{z^3}+\dfrac{z^5}{x^3}\) thì đề bài sai
Biểu thức này chỉ có min, không có max
Thầy ơi làm sao để xác định đề bài tìm Max hay Min ạ?