LT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
13 = (\(x+y\))3 = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 = \(x^3\)+y3+3\(xy\)(\(x+y\))
1 = \(x^3\)+y3+3\(xy\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\)y + 3\(xy\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
NT
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
NT
11 tháng 7 2015
Đăng bài lên để nhờ mọi người giải hộ mà không thấy ai giải hộ cả. Giờ mình cũng đã tìm ra cách giải rồi (không biết có đúng không)
* Theo đề bài ra ta có:
x^2 - y = y^2 - x <=> x^2 - y^2 = y - x <=> (x - y)*(x + y) = y - x <=> x + y = (y - x)/(x - y) (điều kiện x - y # 0)
<=> x + y = -(y - x)/(y - x) = -1 (điều kiện x # y).
<=> x = -y. Ta có 2 trường hợp xảy ra:
T/h1: x = y, khi đó A = x^3 + x^3 + 3x*x(x^2 + x^2) + 6x^2*x^2(x + x) = 2x^3 + 3x^2 * 2x^2 + 6x^4 * 2x = 2x^3 + 6x^4 + 12x^5;
T/h2: x =-y, khi đó A = x^3 + (-x)^3 + 3x*(-x)(x^2 + (-x)^2) + 6x^2*(-x)^2(x + (-x))
= x^3 - x^3 - 3x^2(x^2 + x^2) + 6x^2*x^2(x - x) = -6x^4 + 6x^4 * 0 = -6x^4
ML
8 tháng 8 2015
x2-y=y2-x
<=>(x2-y2)+(x-y)=0
<=>(x-y)(x+y)+(x-y)=0
<=>(x-y)(x+y+1)=0
*)Nếu x-y=0<=>x=y
Tính a theo x ta có
A=x3+x3+3x2(x2+x2)+6x4(x+x)
=2x3+6x4+12x5
*)Nếu x+y+1=0
<=>x=-(y+1)
Tính A theo y ta có
A=(-y-1)3+y3+3(y-1)y[(-y-1)2+y2]+6(-y-1)2y2(-y-1+y)
cái này bạn tự tính
QV
1
19 tháng 12 2015
Ta có:
\(x^3+3xy-y^3=x^3-y^3+3xy=\left(x-y\right)\left(x^2+xy+y^2\right)+3xy\)
\(=-\left(x^2+xy+y^2\right)+3xy=-x^2-xy+y^2+3xy=-x^2+2xy+y^2=y^2+2xy-x^2\)
\(=-\left(y^2-2xy+x^2\right)=-\left(y-x\right)^2=-\left(x-y\right)^2=-\left(-1\right)^2=-1\)
tick đúng nha
M
3
27 tháng 7 2016
\(x^3+y^3+3xy\)
\(=\left(x+y\right)\left(x^2+y^2-xy\right)+3xy\)
Do x + y = 1 nên:
\(=x^2+y^2-xy+3xy\)
\(=x^2+y^2+2xy\)
\(=\left(x+y\right)^2\)
Do x + y = 1 nên:
\(=1^2=1\)
LC
27 tháng 7 2016
Với x+y=1 ta có :
x^3+y^3+3xy
=(x+y)(x^2-xy+y^2)+3xy
=x^2+2xy+y^2
=(x+y)^2=1
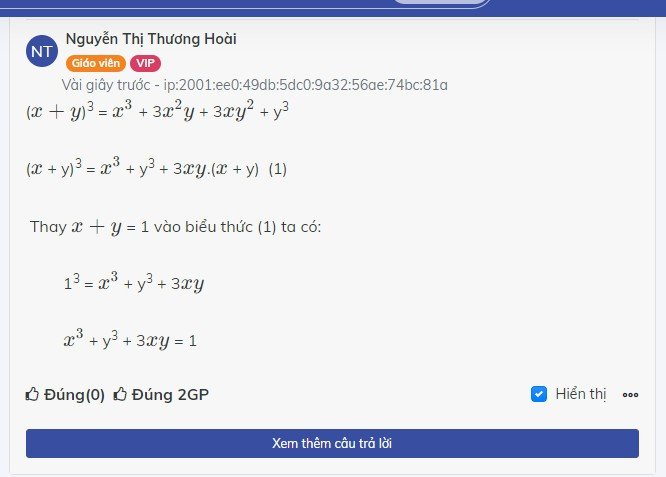
\(P=x^3+3xy+y^3=x^3+3xy\left(x+y\right)+y^3=\left(x+y\right)^3=1^3=1\)