
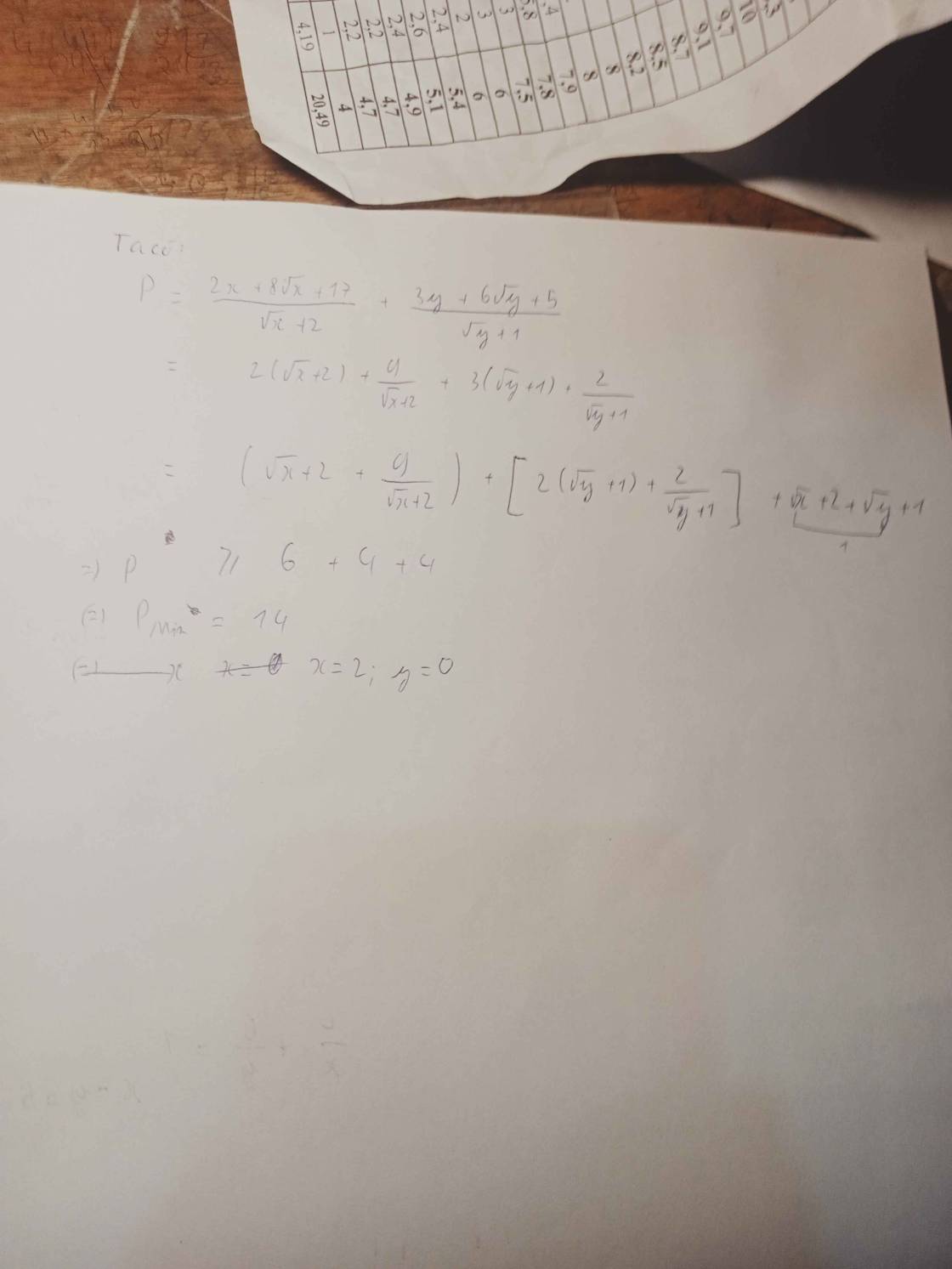
tìm GTNN của biểu t...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

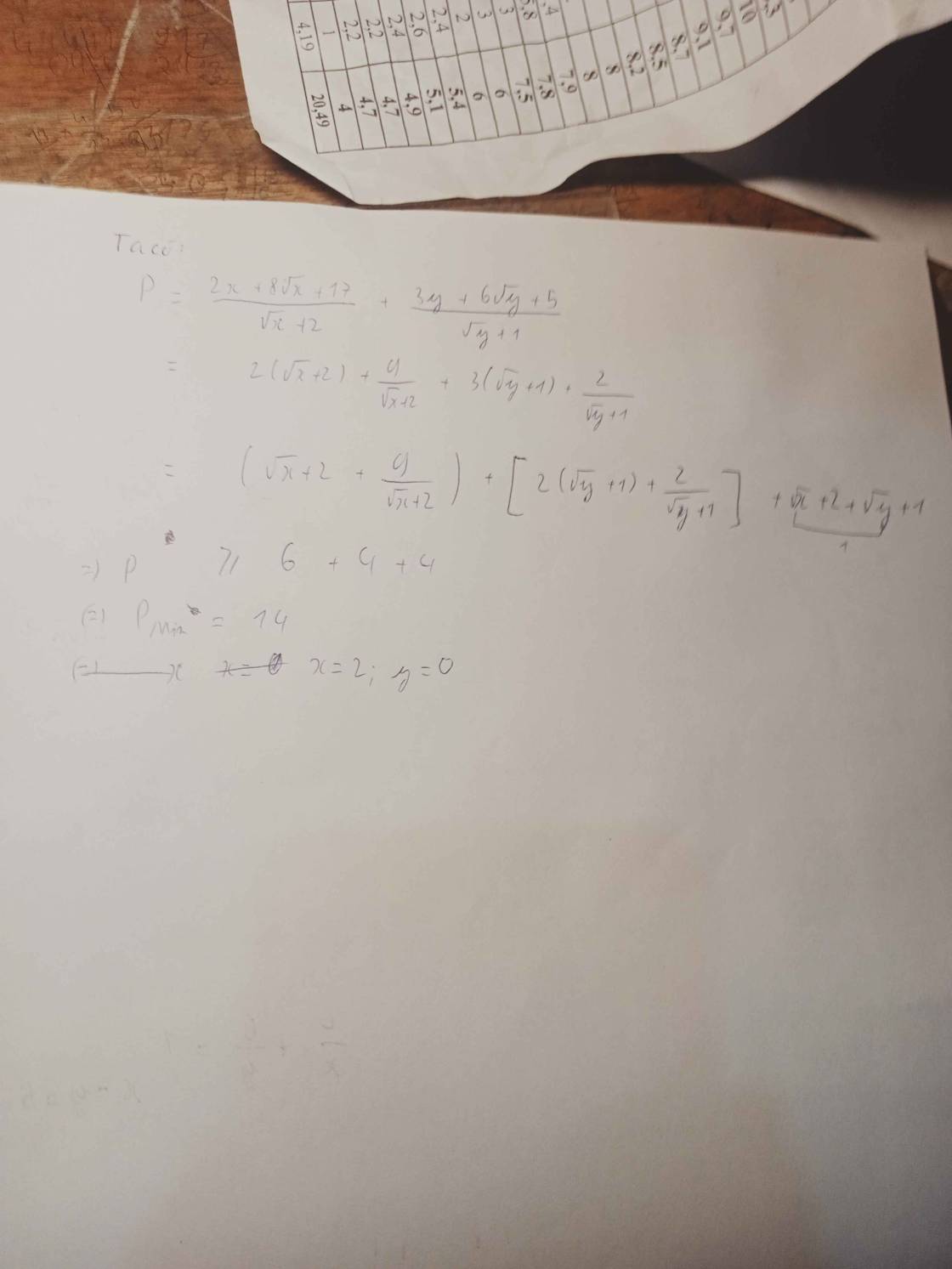

chịu thua vô điều kiện xin lỗi nha : v
muốn biết câu trả lời lo mà sệt trên google ấy đừng có mà dis:v

b, Ta có
\(\frac{\sqrt{x}+1}{y+1}=\frac{\left(\sqrt{x}+1\right)\left(y+1\right)-y-y\sqrt{x}}{y+1}=\sqrt{x}+1-\frac{y\left(\sqrt{x}+1\right)}{y+1}\)
Mà \(y+1\ge2\sqrt{y}\)
=> \(\frac{\sqrt{x}+1}{y+1}\ge\sqrt{x}+1-\frac{1}{2}\sqrt{y}\left(\sqrt{x}+1\right)\)
Khi đó
\(P\ge\frac{1}{2}\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)+3-\frac{1}{2}\left(\sqrt{xy}+\sqrt{yz}+\sqrt{xz}\right)\)
Mà \(\sqrt{xy}+\sqrt{yz}+\sqrt{xz}\le\frac{\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)^2}{3}=3\)
=> \(P\ge\frac{1}{2}.3+3-\frac{3}{2}=3\)
Vậy MinP=3 khi x=y=z=1

\(P=\frac{3x-6\sqrt{x}+7}{2\sqrt{x}-2}+\frac{y-4\sqrt{x}+10}{\sqrt{y}-2}\)
\(=\frac{3\left(\sqrt{x}-1\right)}{2}+\frac{4}{2\left(\sqrt{x}-1\right)}+\left(\sqrt{y}-2\right)+\frac{6}{\sqrt{y-1}}\)
\(=\frac{3\left(\sqrt{x}-1\right)}{2}+\frac{3}{2\left(\sqrt{x}-1\right)}+\left(\sqrt{y}-2\right)+\frac{4}{\left(\sqrt{y}-2\right)}+\frac{4}{2\left(\sqrt{y}-2\right)}+\frac{1}{2\left(\sqrt{x}-1\right)}\)
\(\ge2.\sqrt{\frac{3}{2}.\frac{3}{2}}+2\sqrt{4}+\frac{\left(1+2\right)^2}{2\left(\sqrt{x}+\sqrt{y}-3\right)}\)
\(=3+4+\frac{3}{2}=\frac{17}{2}\)
Dấu "=" xảy ra <=> x = 4 và y = 16