Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) O A t ^ + x O y ^ = 60°+ 120° = 180° (hai góc trong cùng phía bù nhau)
=> At // Oy => tt' // Oy
b) Vì Om là phân giác x O y ^ nên:
x O m ^ = 1 2 x O y ^ = 1 2 .120° = 60° (1)
Mặt khác : O A t ^ = 60 ° = > x A t ^ = 120°
Vì An là phân giác x A t ^ nên:
x A n ^ = 1 2 x A t ^ = 1 2 .120° = 60° (2)
Từ (1) và (2) suy ra x O m ^ = x A n ^ .
Do đó Om // An
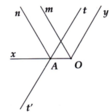

Bạn tự vẽ hình nha![]()
a.
yOA + tAO
= 1200 + 600
= 1800
=> yOA và tAO kề bù
mà 2 góc này ở vị trí trong cùng phía
=> Oy // At
b.
Oy // At
=> AOy = xAt (2 góc đồng vị)
Om là tia phân giác của xOy
=> xOm = mOy = \(\frac{xOy}{2}\)
On là tia phân giác của xAt
=> xAn = nAt = \(\frac{xAt}{2}\)
mà xOy = xAt (chứng minh trên)
=> xAn = xOm
mà 2 góc này ở vị trí đồng vị
=> Om // An
Chúc bạn học tốt![]()
a) ta có: xOy=120 (đề cho) và oAt= 60 (đề cho) ta lại có xOy+tAo=120 + 60 =180 (kề bù) mà 2 góc xOy và tAo ở vị trí trong cùng phía suy ra : oy // At mà AT' là tia đối của tia AT suy ra : tt' // oy
b) ta có xOy = xAt ( 2 góc đồng vị , oy // at ) mà xoy= 120 suy ra xAt=120 vì om là tia phân gica của xOy nên xom = moy = xoy/2 = 60 và on là tia phân giác của xAt xAn=nAt = xAt/2 = 60 mà xOy = xAt ( = 120 ) ta có xAn = xOm (= 60 ) mà 2 góc xAn và xOm ở vị tí đồng vị suy ra : An // Om
các số nhớ thêm độ đấy nhé

a, Vì \(\widehat{xOy}+\widehat{OAt}=180^0\) mà 2 góc này ở vị trí trong cùng phía nên Oy//At
Mà tt' trùng At nên Oy//tt'
b, Vì Om là p/g xOy nên \(\widehat{xOm}=\dfrac{1}{2}\widehat{xOy}\)
Vì An là p/g tAx nên \(\widehat{xAn}=\dfrac{1}{2}\widehat{tAx}=\dfrac{1}{2}\widehat{xOy}\left(đồng.vị\right)\)
Do đó \(\widehat{xOm}=\widehat{xAn}\) mà 2 góc này ở vị trí đồng vị nên Om//An

a: \(\widehat{tAO}+\widehat{xOy}=180^0\)
mà hai góc này trong cùng phía
nên tt'//Oy
b: \(\widehat{xAt}+\widehat{tAO}=180^0\)
=>\(\widehat{xAt}=180^0-60^0=120^0\)
=>\(\widehat{xAn}=\dfrac{120^0}{2}=60^0\)
Om là phân giác của góc xOy
=>\(\widehat{xOm}=\dfrac{1}{2}\cdot120^0=60^0\)
\(\widehat{xOm}=\widehat{xAn}\)
mà hai góc này ở vị trí đồng vị
nên Om//An

Vì xAt + tAO = 180* (kề bù)
=>xAt = 180* - tAO
=> xAt = 180* - 60* = 120* = xOy
mà xAt và xOy là cặp góc đồng vị => song song
b.
Om là tia phân giác của xOy => mOy = xOy :2 = 120* : 2 = 60*
An là tia phân gác của xÁt => xAn = xAt : 2 = 120* : 2 = 60*
=> mOy = xAn = 60*Mà 2 góc này ở vị trí đồng vị => song song

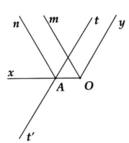
Ta có : xAt + tAy = 180° ( kề bù)
=> tAx = 180° - 60° = 120°
=> xAt = AOy = 120°
Mà 2 góc này ở vị trí đồng vị
=> At//Oy
Mà At' là tia đối At
=> tt' //Oy
b) Vì On là phân giác xAt
=> xAn = tAn = \(\frac{120°}{2}\)= 60°
VÌ Om là phân giác xOy
=> xOn = nOy = \(\frac{120°}{2}\)=60°
=> xAn = AOm = 60°
Mà 2 góc này ở vị trí đồng vị
=> On //Om