
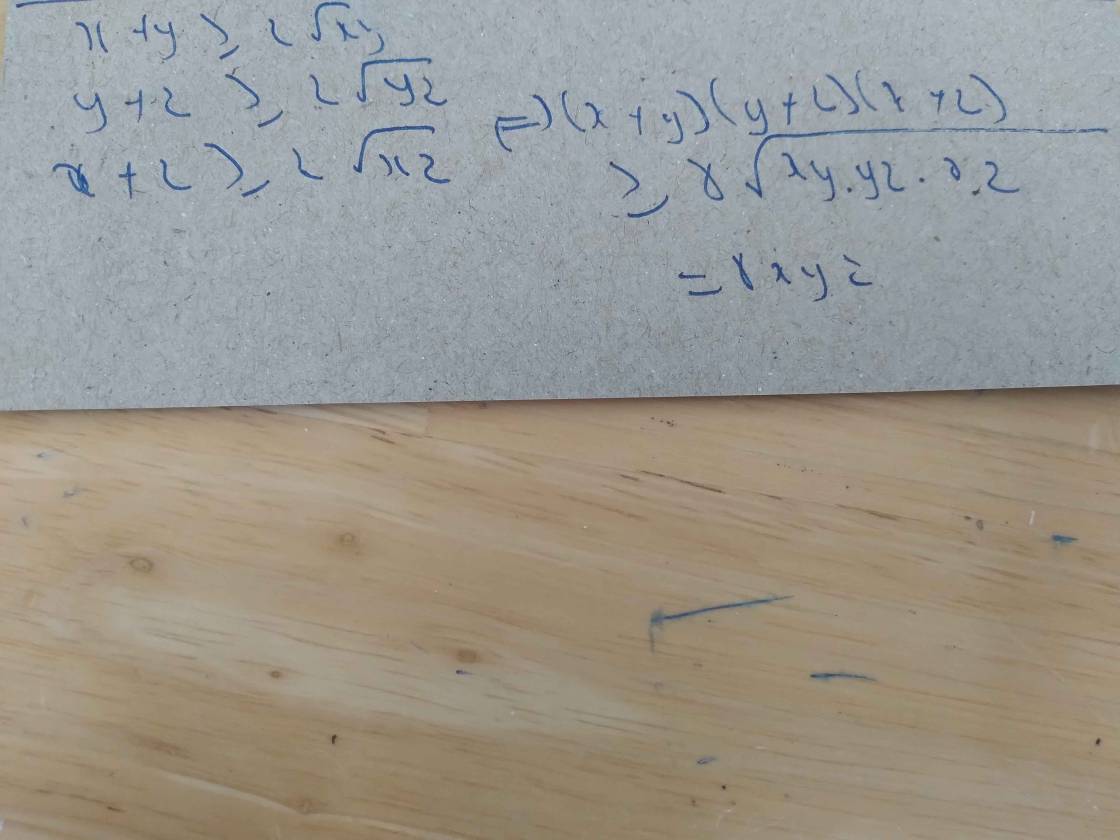
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

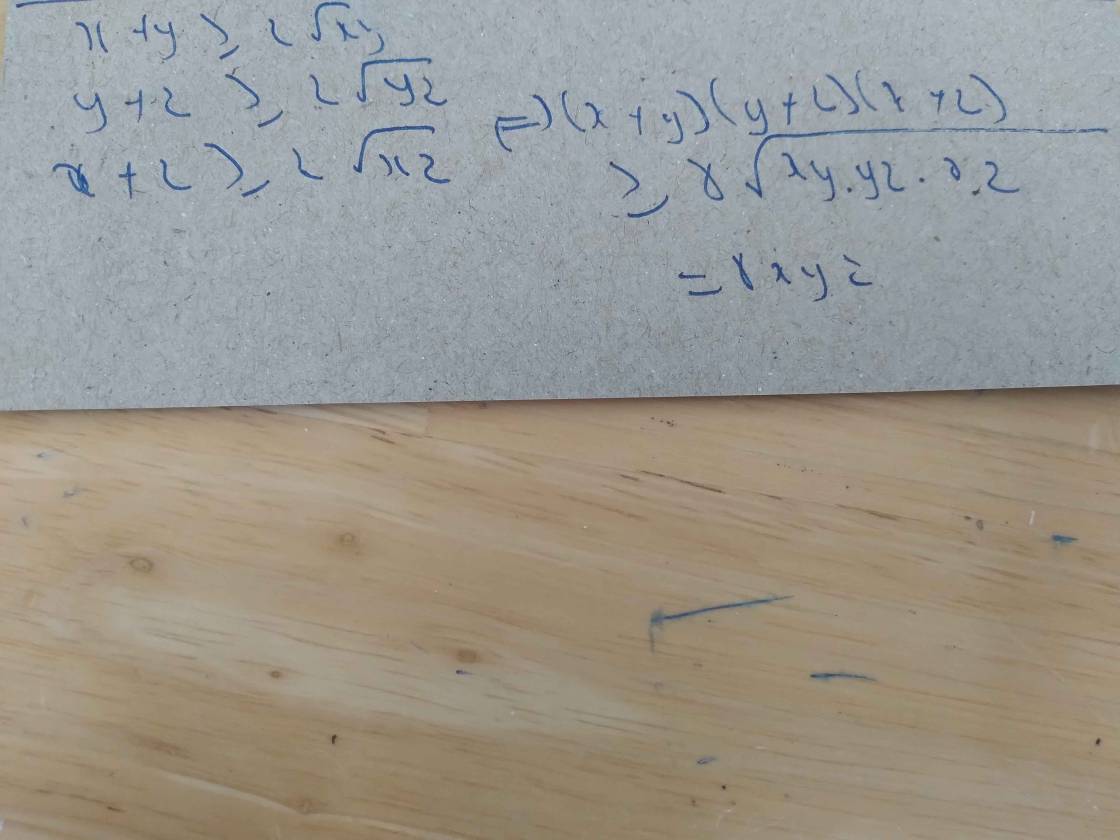


Lần lượt áp dụng bất đẳng thức cô-si ta có: \(x+y\ge2\sqrt{xy};y+z\ge2\sqrt{yz};z+x\ge2\sqrt{zx}.\)
Suy ra: \(\left(x+y\right)\left(y+z\right)\left(z+x\right)\ge2\sqrt{xy}.2\sqrt{yz}.2\sqrt{zx}=8xyz.\)
Dấu bằng xảy ra khi x = y = z.

(x + y)(y + z)(x + z) = 8xyz
⇒ (xy + xz + y2 + yz)(x + z) - 8xyz = 0
⇒ x2y + xyz + x2z + xz2 + y2x + y2z + xyz + yz2 - 8xyz = 0
⇒ x2y - 2xyz + yz2 + xy2 - 2xyz + xz2 + x2z - 2xyz + y2z = 0
⇒ y(x - z)2 + x(y - z)2 + z(x - y)2 = 0
mà x, y, z > 0 (gt)
⇒ \(\left\{{}\begin{matrix}\left(x-z\right)^2=0\\\left(y-z\right)^2=0\\\left(x-y\right)^2=0\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x-z=0\\y-z=0\\x-y=0\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x=z\\y=z\\x=y\end{matrix}\right.\)
⇒ x = y = z

vì x,y,z>0 nên áp dụng bđt côsi ta có
x+y >= 2\(\sqrt{xy}\)
y+z >= 2\(\sqrt{yz}\)
z+x >= 2\(\sqrt{xz}\)
\(\Rightarrow\)(x+y)(y+z)(z+x) >= 8\(\sqrt{x^2y^2z^2}\)
>= 8xyz
Dấu = xảy ra <=> x=y=z


Áp dụng BĐT AM-GM có:
\(\left(x+y\right)\left(y+z\right)\left(z+x\right)\ge2\sqrt{xy}.2\sqrt{yz}.2\sqrt{zx}=8\sqrt{x^2y^2z^2}=8xyz\)
Dấu "=" xảy ra khi x=y=z
\(\Rightarrow\) tam giác ABC là tam giác đều.

bạn tham khảo ở đây: Câu hỏi của Nguyễn Phương Linh - Toán lớp 8 - Học toán với OnlineMath

(x+y)(y+z)(x+z)=8xyz
<=>\((xy+xz+y^2+yz)(x+z)=8xyz\)
<=>\(x^2y+x^2z+y^2z+xyz+xyz+xz^2+z^2y+yz^2=8xyz\)
<=> \(x^2y+x^2z+y^2x+xz^2+y^2z+yz^2-6xyz=0\)
<=> \(y(x^2+z^2-2xz)+x(y^2-2yz+z^2)+z(y^2-2yx+x^2)=0\)
<=>\(y(x-z)^2+x(y-z)^2+z(x-y)^2=0\)
Mà x,y,z dương
=> \((x-z)^2=0=>x=z\)
\((x-y)^2=0=>x=y\)
\((y-z)^2=0=>y=z\)
Vậy x=y=z

\(A=\left(x+y-z\right)\left(y+z-x\right)\left(z+x-y\right)\)
\(áp\) \(dụng\) \(bđt:\) \(\)\(AM-GM:a+b\ge2\sqrt{ab}\Leftrightarrow\sqrt{ab}\le\dfrac{a+b}{2}\Leftrightarrow ab\le\dfrac{\left(a+b\right)^2}{4}\)
\(\Rightarrow A^2=\left(x+y-z\right)^2\left(y+z-x\right)^2\left(z+x-y^2\right)=\left(x+y-z\right)\left(y+z-x\right)\left(y+z-x\right)\left(z+x-y\right)\left(x+y-z\right)\left(z+x-y\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x+y-z\right)\left(y+z-x\right)\le\dfrac{\left(x+y-z+y+z-x\right)^2}{4}\le\dfrac{4y^2}{4}\le y^2\\\left(y+z-x\right)\left(z+x-y\right)\le\dfrac{\left(y+z-x+z+x-y\right)^2}{4}\le z^2\\\left(x+y-z\right)\left(z+x-y\right)\le\dfrac{\left(x+y-z+z+x-y\right)^2}{4}\le x^2\\\end{matrix}\right.\)
\(\)\(\Rightarrow A^2\le x^2y^2z^2\le\left(xyz\right)^2\Rightarrow A\le xyz\)