NN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 2 2022
a: \(B=x\left(x+y\right)\left(x-y\right)\left(x+2y\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+2xy-xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)^2-2y^2\left(x^2+xy\right)+y^4\)
\(=\left(x^2+xy-y^2\right)^2\)
b: \(C=\left(x-y\right)\left(x-4y\right)\left(x-2y\right)\left(x-3y\right)+y^4\)
\(=\left(x^2-5xy+4y^2\right)\left(x^2-5xy+6y^2\right)+y^4\)
\(=\left(x^2-5xy\right)^2+10y^2\left(x^2-5xy\right)+25y^4\)
\(=\left(x^2-5xy+5y^2\right)^2\)
PN
1
15 tháng 8 2020
đặt \(A=x^2+y^2+2x\left(y-1\right)+2y=x^2+y^2+2xy-2x+2y=\left(x+y\right)^2-2\left(x-y\right)\)
do A là số chính phương => \(\left(x+y\right)^2-2\left(x+y\right)\)cũng là số chính phương
\(\Leftrightarrow-2\left(x-y\right)=0\)
\(\Leftrightarrow x=y\)
HB
5
2 tháng 1 2017
Bạn ngonhuminh, chứng minh chỗ (1) sai rồi nhé.
Khi gọi \(d=gcd\left(x-y,2\left(x+y\right)+1\right)\) thì lúc này chưa có \(d=1\).
Vậy \(y^2⋮d\) không suy ra được \(y⋮d\) đâu nha bạn.
Tuy nhiên lời giải có thể sửa lại dễ dàng như sau:
Giả sử \(x-y\) và \(2\left(x+y\right)+1\) không nguyên tố cùng nhau, tức là sẽ có ước NGUYÊN TỐ chung lớn nhất.
Gọi số đó là \(p\). Lúc này \(y^2⋮p\Rightarrow y⋮p\). CM tương tự của bạn suy ra \(p=1\) (vô lí).
Vậy \(x-y\) và \(2\left(x+y\right)+1\) nguyên tố cùng nhau.
2 tháng 1 2017
\(2x^2+x=3y^2+y\Leftrightarrow\orbr{\begin{cases}\left(x-y\right)\left\{2\left(x+y\right)+1\right\}=y^2\left(1\right)\\\left(x-y\right)\left\{3\left(x+y\right)+1\right\}=x^2\left(2\right)\end{cases}}\)
Vế trái là số Cp=> VP cũng phải là số CP
Trước hết Ta c/m hai thừa số VT là nguyên tố cùng nhau
(1) g/s d là ước lớn nhất của (x-y) và 2(x+y)+1 => y cũng phải chia hết d
\(2\left(x+y\right)+1-2\left(x-y\right)=3y+1\Rightarrow d=1\)
(2)g/s d là ước lớn nhất của (x-y) và 3(x+y)+1 => x cũng phải chia hết d
\(3\left(x+y\right)+1+3\left(x-y\right)=6x+1\Rightarrow d=1\)
=>VT là số Cp xẩy hai trường hợp
TH1: cả ba thừa số đó bằng nhau
\(\left(x-y\right)=2\left(x+y\right)+1=3\left(x+y\right)+1\)Nghiệm duy nhất x=y=0 => x-y=0; 2(x+y)+1=3(x+y)+1=1 đều là số Cp
TH2: Cả hai thừa số VT là số Cp (**)
(*) (**) Hiển nhiên đúng=> dpcm
P
2
16 tháng 8 2016
Ta có \(A=\left(x+y\right)\left(x+2y\right)\left(x+3y\right)\left(x+4y\right)+y^4\)
\(=\left(x^2+5xy+4y^2\right)\left(x^2+5xy+6y^2\right)+y^4\)
Đặt \(x^2+5xy+5y^2=t\) thì:
\(A=\left(t-y^2\right)\left(t+y^2\right)+y^4=t^2-y^4+y^4=t^2=\left(x^2+5xy+5y^2\right)^2\)
Vì \(x,y\in Z\) nên \(x^2\in Z,\)\(5xy\in Z,\)\(5y^2\in Z\)\(\Rightarrow\)\(x^2+5xy+5y^2\in Z\)
Vậy A là số chính phương.
AL
22 tháng 1 2017
ta có (x+y)(x+2y)(x+3y)(x+4y)+y^4
=(x+y)(x+4y)(x+2y)(x+3y)+y^4
=(x^2+5xy+4y^2)(x^2+5xy+6y^2)+y^4
đặt x^2+5xy=a
<=>A=a(a+2y^2)+y^4
=a^2+2.a.y^2+y^4
=(a+y^2)^2
là scp
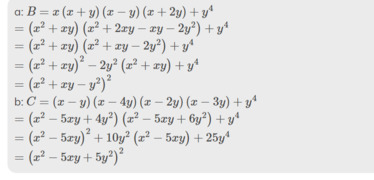
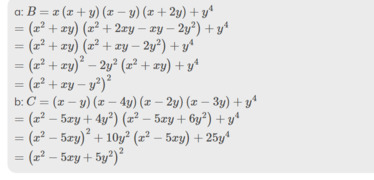
T nghĩ đề thế này chứ nhỉ ???
\(x\left(x+y\right)\left(x+2y\right)\left(x+3y\right)+y^4\)
\(=\left(x^2+3xy\right)\left(x^2+3xy+2y^2\right)+y^4\)
Đặt \(x^2+3xy+y^2=t\) Khi đó:
\(A=\left(t-y^2\right)\left(t+y^2\right)+y^4\)
\(=t^2-y^4+y^4\)
\(=t^2=\left(x^2+3xy+y^2\right)^2\) là số chính phương
Sửa đề:)),
\(A=x\left(x+y\right)\left(x+2y\right)\left(x+3y\right)-y^4\)
\(=x\left(x+3y\right)\left(x+y\right)\left(x+2y\right)-y^4\)
\(=\left(x^2+3xy\right)\left(x^2+3xy+2y^2\right)+y^4\)(1)
Đặt \(x^2+3xy=t\)
\(\Rightarrow\left(1\right)=t\left(t+2y^2\right)+y^4=\left(t+y^2\right)^2\)(2)
Mà \(x^2+3xy=t\)nên \(\left(2\right)=\left(x^2+3xy+y^2\right)^2\)(là scp)