Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì x và y là hai đại lượng tỉ lệ thuận, nên:
y = ax (a là hệ số tỉ lệ, a khác 0)
Khi đó: y1 = a.x1 và y2 = a.x2
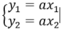
Suy ra y1 + y2 = ax1 + ax2 = a(x1 + x2)
Vậy : y = -5x.

a: x và y là hai đại lượng tỉ lệ thuận
=>\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
mà \(x_1+x_2=2;y_1+y_2=10\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{2}{10}=\dfrac{1}{5}\)
=>\(\dfrac{x}{y}=\dfrac{1}{5}\)
=>y=5x
b: Khi x=1 thì \(y=5\cdot1=5\)

a) Vì x và y là hai đại lượng tỉ lệ thuận, nên :
y = ax (a là hệ số tỉ lệ, a khác 0)
Khi đó : \(\begin{cases} y_1 = ax_1\\ y_2 = ax_2 \end{cases}\)
Suy ra \(y_1+y_2=a\left(x_1+x_2\right)\) => -10 = a.2 => a = -5
Vậy : y = -5x
b) y = 5
trả lời hộ m đi