Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cái đề dài thế này, chả biết khó hay ko nhưng mà ngại làm quá :[
hình như câu b cho đề sai, pải là: ∆EAB=∆ECD mới đúng

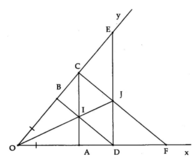
a) Ta có: OD = OB + BD
OC=OA+AC
mà OA=OB; AC=BD
=>OD=OC
Xét 2 TG ODA và OCB;ta có:
OA-OB(gt); O:góc chung; OD=OC(cmt)
=>TG ODA= TG OCB(c.g.c)
=>AD=BC(2 cạnh tương ứng)
b. TG ODA=TG OCB=> góc C=góc D(2 góc tương ứng)
=>OAD=OBC(2 góc tương ứng)
Ta có: OAD+EAC=180
OBC+EBD=180
Từ (1) và (2)=> OAD+EAC=OBC+EBD=180
mà OAD=OBC(cmt)=>EAC=EBD
Xét 2 TG EAC và EBD; ta có:
AC=BD(gt); C=D(cmt); EAC=EBD(cmt)
=>TG EAC=TG EBD (g.c.g)
c. Vì TG EAC=TG EBD=> EA=EB(2 cạnh tương ứng)
Xét TG OBE và OAE, ta có:
OA=OB(gt); EA=EB(cmt); OE:cạnh chung
=>TG OBE=TG OAE(c.c.c)
=>BOE=EOA(2 cạnh tương ứng)
mà OE nằm giữa OA và OB=> OE là phân giác của góc xOy
Không pt đúng ko

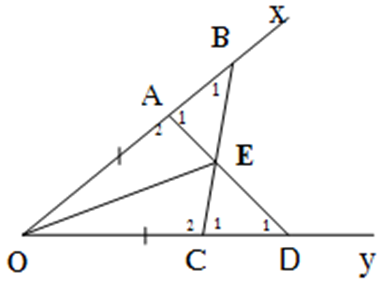
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy

Ta có hình vẽ:
x O y A B C D E
a/ Xét tam giác OAD và tam giác OBC có:
OA = OC (GT)
\(\widehat{O}\): góc chung
OB = OD (GT)
=> tam giác OAD = tam giác OBC (c.g.c)
=> AD = BC (2 cạnh tương ứng)
b/ Ta có: \(\widehat{B}\)=\(\widehat{D}\) (vì tam giác OAD = tam giác OBC) (1)
Ta có: \(\begin{cases}OA=OC\\OB=OD\end{cases}\)\(\Rightarrow AB=CD\) (2)
Ta có: \(\widehat{OAD}\)=\(\widehat{OCB}\) (vì tam giác OAD = tam giác OBC) (*)
+)Ta có: \(\widehat{OAD}\)+\(\widehat{DAB}\)=1800 (**)
+) Ta có: \(\widehat{OCB}\)+\(\widehat{BCD}\)=1800 (***)
Từ (*),(**),(***) => \(\widehat{DAB}\)=\(\widehat{BCD}\) (3)
Từ (1),(2),(3) => tam giác EAB = tam giác ECD
c/ Xét tam giác OAE và tam giác OCE có:
OA = OC (GT)
AE = EC (vì tam giác EAB = tam giác ECD)
OE: cạnh chung
=> tam giác OAE = tam giác OCE (c.c.c)
=> \(\widehat{AOE}\)=\(\widehat{COE}\) (2 góc tương ứng)
=> OE là phân giác \(\widehat{xOy}\) (đpcm)

a) ∆OAD và ∆OCB có: OA= OC(gt)
=
(=
)
OD=OB(gt)
Nên ∆OAD=∆OCB(c.g.c)
suy ra AD=BC.
b) ∆OAD=∆OCB(cmt)
Suy ra: =
=
=>
=
Do đó ∆AOE = ∆OCE(c .c.c)
suy ra: =
vậy OE là tia phân giác của xOy.
b) ∆AEB= ∆CED(câu b) => EA=EC.
∆OAE và ∆OCE có: OA=OC(gt)
EA=EC(cmt)
OE là cạnh chung.
Nên ∆OAE=∆(OCE)(c .c.c)
suy ra: =
vậy OE là tia phân giác của góc xOy.