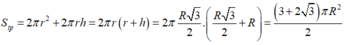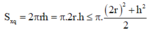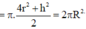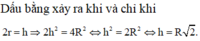K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
3 tháng 5 2018
Chọn đáp án B
+ Gọi h, r lần lượt là chiều cao và bán kính đường tròn đáy của hình trụ.
Khi đó, bán kính mặt cầu ngoại tiếp hình trụ là
![]()
+ Theo bài ra, ta có h = r nên suy ra
![]()
+ Diện tích toàn phần hình trụ là: