Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề bài ta có x = , y =
( a, b, m ∈ Z, m > 0)
Vì x < y nên ta suy ra a< b
Ta có : x = , y =
; z =
Vì a < b => a + a < a +b => 2a < a + b
Do 2a< a +b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a+b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z< y
Hãy chứng tỏ rằngGiả sử x = ; y = ( a, b, m Z, b # 0) và x < y. Hãy chứng tỏ rằng nếu chọn z =∈ thì ta có x < z < yLời giải:Theo đề bài ta có x = , y = ( a, b, m Z, m > 0)∈Vì x < y nên ta suy ra a< bTa có : x = , y = ; z = Vì a < b => a + a < a +b => 2a < a + b

Ta có: \(x< y\Rightarrow\dfrac{a}{m}< \dfrac{b}{m}\Rightarrow a< b\left(m>0\right)\)
\(z=\dfrac{a+b}{2m}>\dfrac{a+a}{2m}=\dfrac{2a}{2m}=\dfrac{a}{m}=x\)
\(z=\dfrac{a+b}{2m}< \dfrac{b+b}{2m}=\dfrac{2b}{2m}=\dfrac{b}{m}=y\)
\(\Rightarrow x< z< y\)

Ta có: \(x< y\Leftrightarrow\dfrac{a}{m}< \dfrac{b}{m}\Leftrightarrow a< b\)(1)
Từ (1), Suy ra:
\(a< b\Leftrightarrow a+a< b+a\Leftrightarrow2a< a+b\left(2\right)\)
\(a< b\Leftrightarrow a+b< b+b\Leftrightarrow a+b< 2b\left(3\right)\)
Từ (2);(3), ta có:
\(2a< a+b< 2b\Leftrightarrow\dfrac{2a}{2m}< \dfrac{a+b}{2m}< \dfrac{2b}{2m}\)
\(\Leftrightarrow x< z< y\left(đpcm\right)\)

Vì x < y
=> a < b
Theo đề bài , ta có :
\(x=\dfrac{a}{m}=\dfrac{2a}{2m}\) ; \(y=\dfrac{b}{m}=\dfrac{2b}{2m}\) ; \(z=\dfrac{a+b}{m}\)
Từ a<b , ta lại có :
a < b => a + a < a + b => 2a < a + b (1)
a < b => a + b < b + c => a + b < 2b (2)
Từ (1) và (2)
=> \(\dfrac{2a}{2m}< \dfrac{a+b}{2m}< \dfrac{2b}{2m}\)
<=> \(x< y< z\)

Có x=a/m; y=b/m và x<y nên a/m<b/m ⇒a<b
Giả sử z>x là đúng thì\(\dfrac{a+b}{2m}>\dfrac{a}{m}\Leftrightarrow\dfrac{a+b}{2m}-\dfrac{a}{m}>0\\ \Leftrightarrow\dfrac{a+b-2a}{2m}>0\Leftrightarrow\dfrac{b-a}{2m}>0\\ m\text{à}b>a;m>0n\text{ê}nz>xl\text{à}\text{đ}\text{úng (1)}\)Giả sử z<y là đúng thì
\(\dfrac{a+b}{2m}< \dfrac{b}{m}\Leftrightarrow\dfrac{a+b}{2m}-\dfrac{b}{m}< 0\\ \Leftrightarrow\dfrac{a+b-2b}{2m}< 0\Leftrightarrow\dfrac{a-b}{2m}< 0\\ m\text{à}a< b;m>0n\text{ê}nz< yl\text{à}\text{đ}\text{úng (2)}\)
Từ (1)và(2) suy ra đpcm

Ta co : x<y =>\(\dfrac{a}{m}< \dfrac{b}{m}\Rightarrow a< b\)
\(x=\dfrac{a}{m}=\dfrac{2a}{2m}\)
\(y=\dfrac{b}{m}=\dfrac{2b}{2m}\)
\(z=\dfrac{2a+1}{2m}\)
do 2a < 2a+1 => \(\dfrac{2a}{2m}< \dfrac{2a+1}{2m}\)=> x<z (1)
a<b => a+1 \(\le\)b
\(\Rightarrow2a+2\le2b\)
\(\Rightarrow2a+1< 2b\)
\(\Rightarrow\dfrac{2a+1}{2m}< \dfrac{2b}{2m}\)
\(\Rightarrow z< y\) (2)
\(Tu\left(1\right)va\left(2\right)\)
\(\Rightarrow x< z< y\)
Gia su x = \(\dfrac{a}{m}\), y = \(\dfrac{b}{m}\) (a,b ∈∈Z ; m>0) va x<y
Hay chung to rang z = \(\dfrac{2a+1}{2m}\) thi ta co x<z<y
Giải
x = \(\dfrac{a}{m}\), y = \(\dfrac{b}{m}\)
mà x < y => a < b
=> \(x=\dfrac{2a}{2m};y=\dfrac{2b}{2m}\)
Ta có : a < b
=> a + a < a + a + 1
=> 2a < 2a + 1
=> \(\dfrac{2a}{2m}< \dfrac{2a+1}{2m}\) hay x < z (1)
Ta có : a < b
=> a + a + 1 < b + b
=> 2a+ 1 < 2b
=> \(\dfrac{2a+1}{2m}< \dfrac{2b}{2m}\) hay z < y (2)
Từ (1) và (2) => x < y <z

Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b nên a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) => x < z < y (đpcm)

Bạn vào đây nhé:
Bài 5 SGK trang 8 - Toán lớp 7 | Học trực tuyến
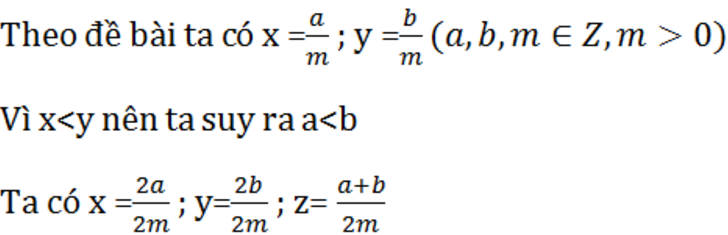
Ta có: x < y \(\Rightarrow\) \(\dfrac{a}{m}\)<\(\dfrac{b}{m}\) \(\Rightarrow\) am < bm (m > 0) \(\Rightarrow\) am + am < bm + am \(\Rightarrow\) 2am < m (b + a) \(\Rightarrow\) \(\dfrac{2a}{m}< \dfrac{a+b}{m}\) \(\Rightarrow\) \(\dfrac{a}{m}< \dfrac{a+b}{m}\). Vậy x < r ( 1 )
T. Tự, ta có: x < y \(\Rightarrow\) \(\dfrac{a}{m}< \dfrac{b}{m}\)\(\Rightarrow\) am < bm (m > 0) \(\Rightarrow\) am + bm < bm + bm \(\Rightarrow\) m ( a + b ) < 2bm \(\Rightarrow\) \(\dfrac{2\left(a+b\right)}{m}< \dfrac{b}{m}\) \(\Rightarrow\dfrac{a+b}{m}< \dfrac{b}{m}\). Vậy r < y (2)
Từ (1) và (2), suy ra : x < r < y .
Lưu ý: Trường hợp này chỉ đúng cho m > 0.
Chúc bn học tốt!!!

