Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do x > 0 nên x 2 > 0 ; 3 x 2 > 0
Áp dụng bất đẳng thức Cô – si cho 3 số dương x 2 ; x 2 ; 3 x 2 ta được:
f x = x + 3 x 2 = x 2 + x 2 + 3 x 2 ≥ 3 . x 2 . x 2 . 3 x 2 3 = 3 . 3 4 3

a,M=0
<=>(x-1)2.(x+2)=0
=>TH1:x-1=0 <=> x=1
=>TH2:x+2=0<=> x=-2
Vậy với x=1 hoặc x=-2 thì M=0
b,M>0
<=>(x-1)2.(x+2)>0
=>TH1: x-1 >0 ; x+2>0
<=> x>1 ; x>-2
=> x>1
=>TH2: x-1 <0 ; x+2<0
<=> x<1 ; x<-2
<=> x<-2
Vậy với x >1 hoặc x<-2 thì M>0
c,M<0
<=>(x-1)2.(x+2)<0
=>TH1 : x-1 >0 ; x+2 <0
<=> x>1 ; x<-2
=> Không có giá trị x
=>TH2: x-1 <0 ; x+2 >0
<=> x<1 ; x>-2
=> -2<x<1
Vậy với -2<x<1 thì M<0
tìm giá trị nhỏ nhất của hàm số: \(y=x^2-3x-4\sqrt{x^2-3x+4}\) với \(x\in\left[1;4\right]\)

Đặt t=\(\sqrt{x^2-3x+4}\)
ta có t \(\in\)(\(\sqrt{2}\) ;\(2\sqrt{2}\))
suy ra y = \(t^2-4t-4\) = \(\left(t-2\right)^2-8\) \(\ge-8\)
Đặt \(t=\sqrt{x^2-3x+4}\).
Ta có hàm số có dạng: \(y=t^2-4t-4\)(*) trên \(\left[1;4\right]\)
Đỉnh \(I\left(2;-8\right)\)
Hàm số đạt GTNN khi \(t=2\Leftrightarrow\sqrt{x^2-3x+4}=2\Leftrightarrow x^2-3x=0\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=3\left(tm\right)\end{matrix}\right.\)
Vậy hàm số (*) đạt GTNN trên \(\left[1;4\right]\) là -8 khi x=3

Với x > 1 thì x -1 >0 .
Áp dụng bất đẳng thức Cô- si ta có:
f x = x 2 + 2 x - 1 = x - 1 2 + 2 x - 1 + 1 2 ≥ 2 . x - 1 2 . 2 x - 1 + 1 2 ⇔ f x ≥ 2 + 1 2 = 5 2
Giá trị nhỏ nhất của hàm số f x = x 2 + 2 x - 1 v ớ i x > 1 là 5 2
Dấu “=’ xảy ra khi x - 1 2 = 2 x - 1 ⇔ x - 1 2 = 4 ⇔ x = 3 > 1

a) Xét \(\Delta\) = b2 - 4ac = (-m)2 - 4(2m - 4)
= m2 - 8m + 16 = ( m - 4 )2
Ta có: ( m - 4 )2 \(\ge\) 0
=> Pt luôn có nghiệm
b) Vì phương trình luôn có nghiệm nên áp dụng định lí Ta- lét:
\(\left\{{}\begin{matrix}x_1+x_2=\frac{-b}{a}==m\\x_1x_2=2m-4\end{matrix}\right.\)
Xét phương trình: x12 + x22 - 9
= x12 + x22 + 2x1x2 - 2x1x2 - 9
= (x1 + x2)2 - 2x1x2 - 9
= (-m)2 - 2(2m - 4) - 9
= m2 - 4m + 8 - 9
= m2 - 4m - 1 = m2 - 4m + 4 - 5
= (m - 2)2 - 5
Xét (m - 2)2 \(\ge\) 0
=> (m - 2)2 - 5 \(\ge\) -5
Dấu " =" xảy ra khi m - 2 = 0
<=> m = 2
\(\Delta=m^2-8m+16=\left(m-4\right)^2\ge0\Rightarrow\) pt luôn có nghiệm
Khi đó theo Viet \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=2m-4\end{matrix}\right.\)
\(A=x_1^2+x_2^2-9=\left(x_1+x_2\right)^2-2x_1x_2-9\)
\(A=m^2-2\left(2m-4\right)-9\)
\(A=m^2-4m-1\)
\(A=\left(m-2\right)^2-5\ge-5\)
\(\Rightarrow A_{min}=-5\) khi \(m=-2\)

Ta có \(\Delta'=1-m\ge0\)=>\(m\le1\)
Theo viet ta có
\(x_1+x_2=2\)
Vì x1 là nghiệm của phương trình
=> \(x_1^2=2x_1-m\)
Khi đó
\(P=\frac{m^3-m^2+4m}{2\left(x_1+x_2\right)+m^2-m}+m^2+1\)
\(=\frac{m\left(m^2-m+4\right)}{m^2-m+4}+m^2+1=m^2+m+1=\left(m+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Vậy \(MinP=\frac{3}{4}\)khi \(m=-\frac{1}{2}\)(thỏa mãn \(x\le1\))
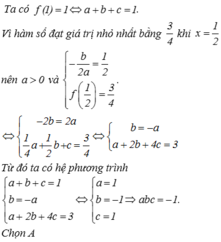



Do x> 0 nên 2x >0 và 3 x > 0 .
Áp dụng bất đẳng thức Cô- si cho 2 số dương: 2 x ; 3 x
f x = 2 x + 3 x ≥ 2 . 2 x . 3 x = 2 6
Dấu “=” xảy ra khi 2 x = 3 x ⇔ x = 3 2 = 6 2 .