Cho x > 0. Chứng minh x + 1 x ≥ 2 . Từ đó tìm giá trị nhỏ nhất của x + 1...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

31 tháng 7 2019

Cho x > 0. Chứng minh x + 1 x ≥ 2 . Từ đó tìm giá trị nhỏ nhất của x + 1 x

#Toán lớp 8

Cao Minh Tâm

31 tháng 7 2019

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

5 tháng 12 2017

Cho x ≥ 2 . Chứng minh x + 1 x ≥ 5 2 . Từ đó tìm giá trị nhỏ nhất của x + 1 x .

#Toán lớp 8

Cao Minh Tâm

5 tháng 12 2017

Đúng(0)

Nao Tomori

28 tháng 8 2015 - olm

a/ chứng minh rằng nếu tổng cảu hai số nguyên chia hết cho 3 thì tổng các lập phương của chúng chia hết cho 3

b/ tìm các giá trị của x để biểu thức: P=(x-1)(x+2)(x+3)(x+6) có giá trị nhỏ nhất. tìm giá trị nhỏ nhất đó

#Toán lớp 8

Nao Tomori

28 tháng 8 2015

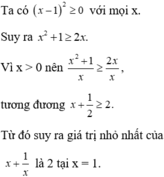
tự biên tự diễn thôi:

a/ gọi 2 số phải tìm là a và b, ta có a+b chia hết cho 3

ta có a^3+b^3=(a+b)(a^2-ab+b^2)=(a+b)[(a^2+2ab+b^2)-3ab]= (a+b)[(a+b)^2-3ab]0,5

vì a+b chia hết cho 3 nên (a+b)^2-3ab chia hết cho 3

do vậy (a+b)[(a+b)^2-3ab] chia hết cho 3

ai làm câu b

Đúng(0)

Tuyết Ly

19 tháng 3 2022

Cho 2 biểu thức A = 3x+2/x và B = x^2+1/x^2−x − 2/x−1 với x≠0, 1.

a) Tính giá trị của biểu thức A khi x = 2/3.

b) Chứng minh B = x−1/x .

c) Đặt P = A: B. Tìm x nguyên để P có giá trị nguyên nhỏ nhất.

#Toán lớp 8

Nguyễn Lê Phước Thịnh

12 tháng 1

Đúng(0)

Tuyết Ly

19 tháng 3 2022

Cho 2 biểu thức A = 3x+2/x và B = x^2+1/x^2−x − 2/x−1 với x≠0, 1.

a) Tính giá trị của biểu thức A khi x = 2/3.

b) Chứng minh B = x−1/x .

c) Đặt P = A: B. Tìm x nguyên để P có giá trị nguyên nhỏ nhất.

#Toán lớp 8

Nguyễn Lê Phước Thịnh

11 tháng 1

a: Thay x=2/3 vào A, ta được:

\(A=\dfrac{3\cdot\dfrac{2}{3}+2}{\dfrac{2}{3}}=\dfrac{2+2}{\dfrac{2}{3}}=4\cdot\dfrac{3}{2}=6\)

b: \(B=\dfrac{x^2+1}{x^2-x}-\dfrac{2}{x-1}\)

\(=\dfrac{x^2+1}{x\left(x-1\right)}-\dfrac{2}{x-1}\)

\(=\dfrac{x^2+1-2x}{x\left(x-1\right)}\)

\(=\dfrac{\left(x-1\right)^2}{x\left(x-1\right)}=\dfrac{x-1}{x}\)

c: P=A:B

\(=\dfrac{3x+2}{x}:\dfrac{x-1}{x}=\dfrac{3x+2}{x}\cdot\dfrac{x}{x-1}=\dfrac{3x+2}{x-1}\)

Để P là số nguyên thì \(3x+2⋮x-1\)

=>\(3x-3+5⋮x-1\)

=>\(5⋮x-1\)

=>\(x-1\in\left\{1;-1;5;-5\right\}\)

=>\(x\in\left\{2;0;6;-4\right\}\)

Kết hợp ĐKXĐ, ta được: \(x\in\left\{2;6;-4\right\}\)

Thay x=2 vào P, ta được:

\(P=\dfrac{3\cdot2+2}{2-1}=\dfrac{8}{1}=8\)

Thay x=6 vào P, ta được:

\(P=\dfrac{3\cdot6+2}{6-1}=\dfrac{18+2}{5}=\dfrac{20}{5}=4\)

Thay x=-4 vào P, ta được:

\(P=\dfrac{3\cdot\left(-4\right)+2}{-4-1}=\dfrac{-12+2}{-5}=\dfrac{-10}{-5}=2\)

Vì 2<4<8

nên khi x=-4 thì P có giá trị nguyên nhỏ nhất

Đúng(0)

Nguyễn Ngọc Thảo Linh

8 tháng 1 2022

a) Tìm số a để đa thức x² + 5x + a chia hết cho đa thức x - 1

b) Chứng minh rằng: x² – x + 1 > 0 với mọi số thực x?

c) Tìm giá trị nhỏ nhất của biểu thức A = x² – 6x + 11

d) Tìm giá trị lớn nhất của biểu thức B = – x² + 4x – 5

#Toán lớp 8

Nguyễn Lê Phước Thịnh

8 tháng 1 2022

b: \(x^2-x+1=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)

c: \(A=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\forall x\)

Dấu '=' xảy ra khi x=3

d: \(B=-\left(x^2-4x+5\right)=-\left(x^2-4x+4+1\right)=-\left(x-2\right)^2-1\le-1\forall x\)

Dấu '=' xảy ra khi x=2

Đúng(0)

Châu Thùy Dương

20 tháng 10 2019 - olm

a)chứng minh x^2-x+1/4 >0
b)tìm giá trị nhỏ nhất x^2-x+1/4
Cảm ơn các bạn

#Toán lớp 8

Nguyễn Chi Linh

20 tháng 10 2019

a)Ta có:

A=x²-x+\(\frac{1}{4}\)=x²-x+(\(\frac{1}{2}\))²=(x-\(\frac{1}{2}\))²\(\ge\)0 \(\forall\)x

b)Ta có A\(\ge\)0

Dấu ''='' xảy ra <=>x-\(\frac{1}{2}\)=0

<=>x =\(\frac{1}{2}\)

Vậy giá trị nhỏ nhất của A bằng 0 <=> x=\(\frac{1}{2}\)

Chúc bạn học tốt

Đúng(0)

Phạm Thị Hạnh

10 tháng 10 2017 - olm

bài 1a)cho x+2y =1. Tìm giá trị nhỏ nhất của x^2+2y^2b)tìm giá trị nhỏ nhất của P=(x-2012)^2+(x+2013)^2c)cho a,b,c>0, 1/1+a+1/1+b+1/1+c=2 tính giá trị lớn nhất của Q=abcbài 2:a)cho a,b,c thuộc Z, chứng minh a^5+b^5+c^5-(a+b+c) chia hết cho 30 b)cho x,y,z >0 thỏa mãn x+y+z=3 chứng minh 1/x^2+x+1/y^2+y+1/z^2+z lớn hơn hoặc bằng 3/2Các cậu ơi giúp mình vs ạ mình cần gấp, cảm ơn các cậu...

Đọc tiếp

#Toán lớp 8

PhongC_VN

20 tháng 12 2021

Cho biểu thức : A = \(\dfrac{x^2+2}{x^2-1}+\dfrac{x+1}{x^2+x+1}+\dfrac{1}{1-x}\)với x ≠ 1
a) Chứng minh A = \(\dfrac{x+1}{x^2+x+1}\)
b) Tìm x để A = \(\dfrac{2}{7}\)
c) Tìm giá trị nhỏ nhất của A

#Toán lớp 8

Nguyễn Lê Phước Thịnh

20 tháng 12 2021

a: \(A=\dfrac{x^2+2+x^2-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2-x}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x}{x^2+x+1}\)

Đúng(1)

Trangg

21 tháng 2 2019 - olm

Cho phương trình x²-mx+m-1=0 (ẩn x, tham số m )

a)giải phương trình với m=3

b)chứng tỏ phường trình luôn có nghiệm với mọi giá trị m

c)gọi x₁ và x₂ là 2 nghiệm của phương trình . Tìm m để biểu thức A=x²₁ +x₂²-4x₁x₂ đạt giá trị nhỏ nhất. tìm giá trị nhỏ nhất đó

#Toán lớp 8

Nguyễn Trần Gia Linh

11 tháng 5 2020

Tui hổng biết

Đúng(0)

Bùi Phương Huyền

11 tháng 5 2020

Tui hổng biết

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP