Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBCD vuông tại B và ΔBEA vuông tại B có
BC=BE
BD=BA
=>ΔBCD=ΔBEA
=>CD=EA
góc DCA+góc EAB=90 độ
=>DC vuông góc AE
b: Kẻ MF vuông góc AC, IE vuông góc AC,NH vuông góc AC
=>MF//BE; IG//BE; NH//BE
MF=EB/2=BC/2
NH=AB/2
NMFH là hình thang nên IG là đường trung bình
=>IG=AC/4 ko đổi

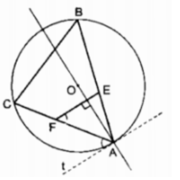
a) Để tính BFD, ta có thể sử dụng tính chất của các tam giác vuông. Vì BF và FD là hai cạnh vuông góc với nhau, nên ta có thể sử dụng định lý Pythagoras để tính độ dài cạnh BD. Sau đó, ta sẽ tính tỉ lệ giữa cạnh BF và cạnh BD để tìm độ dài cạnh BFD.
b) Để chứng minh FC là phần giác của BPD, ta có thể sử dụng các định lý về góc và đường thẳng. Ta cần chứng minh rằng góc FCB bằng góc BPD. Để làm điều này, ta có thể sử dụng các định lý về góc đồng quy và góc nội tiếp.
c) Để chứng minh ST vuông góc với CF, ta có thể sử dụng các định lý về góc và đường thẳng. Ta cần chứng minh rằng góc STF bằng góc CFB. Để làm điều này, ta có thể sử dụng các định lý về góc đồng quy và góc nội tiếp.

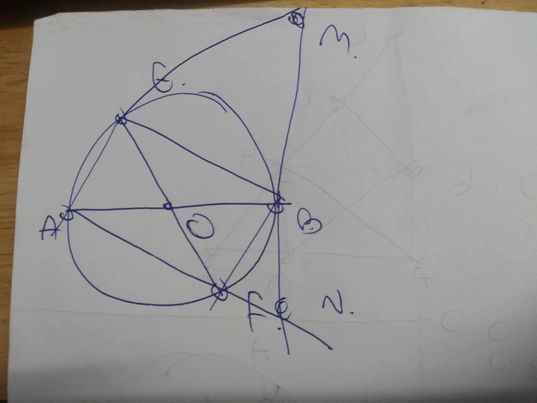

Ta có hình vẽ sau:
Vì ▲ACE có BD // EC; D ∈ AE và B ∈ AC nên ta có:
\(\frac{AB}{AC}=\frac{AD}{AE} \) (Định lý Talet)
Vì ▲AFE có CD // EF; D ∈ AE và C ∈ AF nên ta có:
\(\frac{AC}{AF}=\frac{AD}{AE} \) (Định lý Talet)
Do đó, ta có: \(\frac{AB}{AC} = \frac{AC}{AF} (=\frac{AD}{AE}) \) \(⇔ AC^2 = AB . AF\)
\(\Leftrightarrow\left[{}\begin{matrix}AC=\sqrt{AB.AF}\\AC=\dfrac{AB.AF}{AC}\end{matrix}\right.\)
\(\Leftrightarrow\sqrt{AB.AF}=\dfrac{AB.AF}{AC}\left(=AC\right)\)(Điều phải chứng minh)
Cảm ơn cậu !!