Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

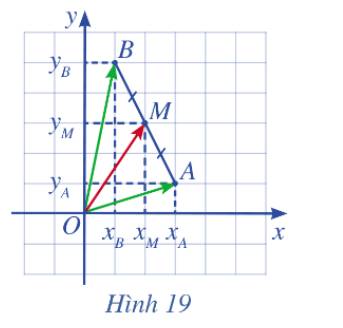
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

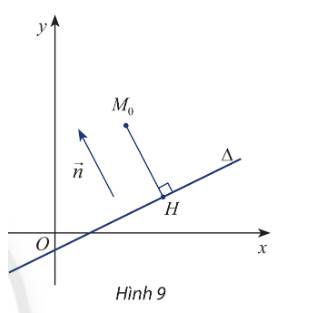
a) Ta có: \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Mà H là hình chiếu vuông góc của \({M_0}\) trên \(\Delta \) nên \(H{M_0} \bot \Delta \)
Mặt khác vectơ pháp tuyến \(\overrightarrow n \) cùng vuông góc với \(\Delta \)
Suy ra \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \)cùng phương (đpcm)
b) Ta có: \(\overrightarrow n = (a;b)\) và \(\overrightarrow {H{M_0}} = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)\)
Suy ra \(p = \overrightarrow n .\overrightarrow {H{M_0}} = a\left( {{x_0} - {x_H}} \right) + b\left( {{y_0} - {y_H}} \right) = a{x_0} + b{y_0} - \left( {a{x_H} + b{y_H}} \right)\) (1)
Mà H thuộc đường thẳng \(\Delta \) nên tọa độ điểm H thỏa mãn phương trình đường thẳng \(\Delta \)
Thay tọa độ điểm H vào phương trình \(\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)\) ta có:
\(a{x_H} + b{y_H} + c = 0 \Leftrightarrow c = - \left( {a{x_H} + b{y_H}} \right)\)
Thay \(c = - \left( {a{x_H} + b{y_H}} \right)\) vào (1) ta có
\(p = a{x_0} + b{y_0} + c\) (đpcm)
c) Ta có: \(p = \overrightarrow n .\overrightarrow {H{M_0}} \Leftrightarrow \overrightarrow {H{M_0}} = \frac{p}{{\overrightarrow n }} \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \left| {\frac{p}{{\overrightarrow n }}} \right| \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}\)

Từ giả thiết ta có:
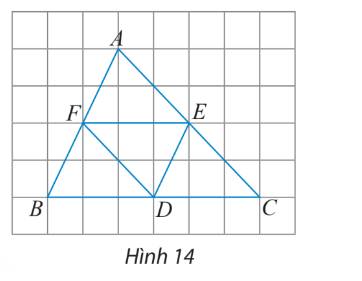
\(AF = FB = ED\); \(AE = EC = FD\); \(BD = DC = EF\)
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ \(\overrightarrow {EF} \)là \(\overrightarrow {DB} \) và \(\overrightarrow {CD} \)
b) Các vectơ đối vectơ \(\overrightarrow {EC} \) là \(\overrightarrow {EA} \) và \(\overrightarrow {DF} \)

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

\(\left| {\overrightarrow a + \overrightarrow b } \right| = 0 \Leftrightarrow \overrightarrow a + \overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow a = - \overrightarrow b \)
\(\overrightarrow a = - \overrightarrow b \) suy ra hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là hai vecto đối nhau nên chúng cùng phương, ngược hướng và có độ dài bằng nhau.

a) Vì \(\overrightarrow {OA} = \overrightarrow u = (x;y)\) nên A(x; y).
Tương tự: do \(\overrightarrow {OB} = \overrightarrow v = \left( {x';y'} \right)\) nên B (x’; y’)
b) Ta có: \(\overrightarrow {OA} = (x;y) \Rightarrow O{A^2} = {\left| {\overrightarrow {OA} } \right|^2} = {x^2} + {y^2}.\)
Và \(\overrightarrow {OB} = (x';y') \Rightarrow O{B^2} = {\left| {\overrightarrow {OB} } \right|^2} = x{'^2} + y{'^2}.\)
Lại có: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = \left( {x';y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\)
\( \Rightarrow A{B^2} = {\left| {\overrightarrow {AB} } \right|^2} = {\left( {x' - x} \right)^2} + {\left( {y' - y} \right)^2}.\)
c) Theo định lí cosin trong tam giác OAB ta có:
\(\cos \widehat O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)
Mà \(\overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = OA.OB.\cos \widehat O\)
\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = OA.OB.\frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{2}\)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{{x^2} + {y^2} + x{'^2} + y{'^2} - {{\left( {x' - x} \right)}^2} - {{\left( {y' - y} \right)}^2}}}{2}\\ \Leftrightarrow \overrightarrow {OA} .\overrightarrow {OB} = \frac{{ - \left( { - 2x'.x} \right) - \left( { - 2y'.y} \right)}}{2} = x'.x + y'.y\end{array}\)

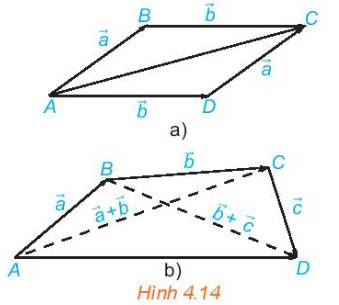
a) Ta có: \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \) nên \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Mặt khác: \(\overrightarrow {AD} = \overrightarrow b ,\;\overrightarrow {DC} = \overrightarrow a \) nên \(\overrightarrow b + \overrightarrow a = \overrightarrow {AD} + \overrightarrow {DC} = \overrightarrow {AC} \)
Do đó \(\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \).
b) Theo câu a) ta có \(\overrightarrow a + \overrightarrow b = \overrightarrow {AC} \) và \(\overrightarrow {CD} = \overrightarrow c \) nên \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \).
Mặt khác: \(\overrightarrow {BC} = \overrightarrow b ,\;\overrightarrow {CD} = \overrightarrow c \) nên \(\overrightarrow b + \overrightarrow c = \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {BD} \)
Và \(\overrightarrow a = \overrightarrow {AB} \) nên \(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right) = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
Vậy \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)

a) \(\overrightarrow{a}+\overrightarrow{b}=\left(2;-2\right)+\left(1;4\right)=\left(3;2\right)\).
\(\overrightarrow{a}-\overrightarrow{b}=\left(2;-2\right)-\left(1;4\right)=\left(1;-6\right)\).
\(2\overrightarrow{a}+3\overrightarrow{b}=2\left(2;-2\right)+3\left(1;4\right)=\left(4;-4\right)+\left(3;12\right)\)\(=\left(7;8\right)\).
c) Gọi x và y là hai số thực để:
\(\overrightarrow{c}=x\overrightarrow{a}+y\overrightarrow{b}=x\left(2;-2\right)+y\left(1;4\right)=\left(2x+y;-2x+4y\right)\)
Từ đó suy ra: \(\left\{{}\begin{matrix}2x+y=5\\-2x+4y=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\).
Vậy \(\overrightarrow{c}=2\overrightarrow{a}+1\overrightarrow{b}\).

\(\left|\overrightarrow{a}+\overrightarrow{b}\right|^2=\left(\overrightarrow{a}+\overrightarrow{b}\right)\left(\overrightarrow{a}+\overrightarrow{b}\right)\)
\(=\left|\overrightarrow{a}\right|^2+\left|\overrightarrow{b}\right|^2+2\overrightarrow{a}.\overrightarrow{b}\)
\(=5^2+12^2+2.5.12.cos\left(\overrightarrow{a},\overrightarrow{b}\right)\)
\(=169+120cos\left(\overrightarrow{a},\overrightarrow{b}\right)=13^2\)
Suy ra: \(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=0\).
\(\overrightarrow{a}\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left(\overrightarrow{a}\right)^2+\overrightarrow{a}.\overrightarrow{b}=5^2+5.12.0=25\).
Mặt khác \(\overrightarrow{a}\left(\overrightarrow{a}+\overrightarrow{b}\right)=\left|\overrightarrow{a}\right|.\left|\overrightarrow{a}+\overrightarrow{b}\right|.cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)\)
\(=5.13.cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)\).
Vì vậy \(25=5.13.cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)\).
\(cos\left(\overrightarrow{a},\overrightarrow{a}+\overrightarrow{b}\right)=\dfrac{5}{13}\).
Vậy góc giữa hai véc tơ \(\overrightarrow{a}\) và \(\overrightarrow{a}+\overrightarrow{b}\) là \(\alpha\) sao cho \(cos\alpha=\dfrac{5}{13}\).
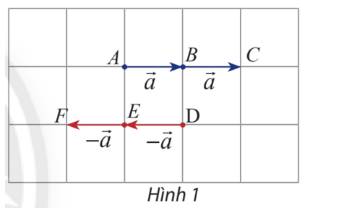

Dựa vào hình 1 ta thấy
Vectơ \(\overrightarrow a + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)
Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)