Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

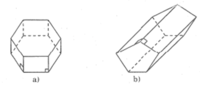
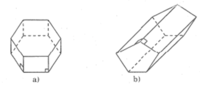
| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Không thể làm một hình lăng trụ đứng có 15 đỉnh vì d = 2n (số đỉnh của hình lăng trụ là một số chẵn)

a: \(mp\left(EFGH\right);mp\left(ABCD\right)\)
\(mp\left(ABFE\right);mp\left(CDHG\right)\)
\(mp\left(ADHE\right);mp\left(BCGF\right)\)
b: Các điểm D,H,G,C cùng thuộc mặt phẳng CDHG
c: Các điểm D,H,G,F không thuộc cùng một mặt phẳng
d: A,B,G,H cùng thuộc mặt phẳng ABGH

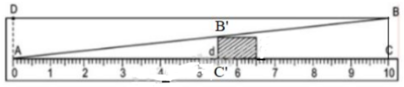
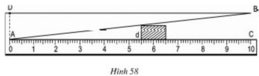
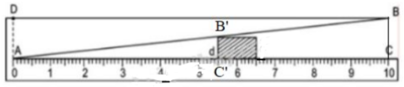
Theo hình vẽ và dựa vào định lí hai tam giác đồng dạng ta có:
ΔABC 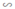 ΔAB’C’ (vì B’C’ // BC).
ΔAB’C’ (vì B’C’ // BC).
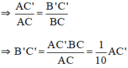
(Vì AC = 10cm, BC = 1cm).
Vậy khi đọc AC’ = 5,5cm thì bề dày của vật B’C’ = 5,5mm.
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì các cạnh tương ứng tỉ lệ.

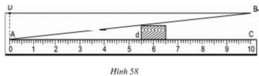
Theo hình vẽ và dựa vào định lí hai tam giác đồng dạng ta có:
ΔABC 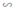 ΔAB’C’ (vì B’C’ // BC).
ΔAB’C’ (vì B’C’ // BC).
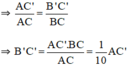
(Vì AC = 10cm, BC = 1cm).
Vậy khi đọc AC’ = 5,5cm thì bề dày của vật B’C’ = 5,5mm.
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì các cạnh tương ứng tỉ lệ.

| Hình lăng trụ | Số cạnh của một đáy (n) | Số mặt (m) | Số đỉnh (d) | Số cạnh (c) |
| a) | 6 | 8 | 12 | 18 |
| b) | 5 | 7 | 10 | 15 |
Số cạnh của một đáy là: n = d/2 = 20/2 = 10 cạnh
Hình lăng trụ có 20 đỉnh thì :
Số mặt là m = n + 2 = 10 + 2 = 12 mặt
Số cạnh là c = 3n = 3.10 = 30 cạnh

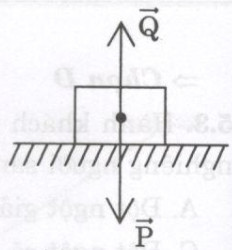
a) Vật đứng yên trên mặt bàn vì \(\overrightarrow{P},\overrightarrow{Q}\) tác dụng lên vật cân bằng nhau.
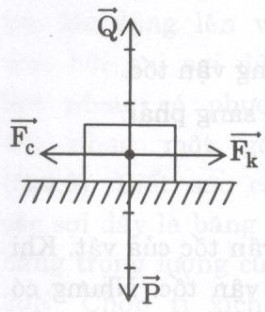
b) Vật chuyển động thẳng đều trên mặt sàn nằm ngang nhờ lực kéo có cường độ 2N. Điều này chứng tỏ lực kéo cân bằng với lực cản của sàn tác dụng lên vật.

\(1.\)
\(\text{*)}\) Ở phương trình phản ứng hóa học đầu tiên, ta nhận thấy có một chất phản ứng (tham gia) và hai chất sinh ra (sản phẩm) nên ta nghĩ ngay đến phản ứng phân hủy, do đó ta có thể biển đổi như sau:
\(2KClO_3\) \(\rightarrow^{t^o}\) \(3O_2\uparrow+2KCl\)
Khi đó, \(A.\) \(O_2\) và \(B.\) \(KCl\)
\(\text{*)}\) Xét ở phương trình hóa học thứ tư, vì có chất phản ứng là \(Zn\) và sản phẩm là \(Zn_3\left(PO_4\right)_2\) nên chắc rằng chữ cái \(F\) phải có công thức hóa học chứa nhóm nguyên tử \(PO_4\), khi đó, ta nghĩ ngay đến \(H_3PO_4\). Thử vào phương trình trên, ta được:
\(3Zn+2H_3PO_4\) \(\rightarrow\) \(Zn_3\left(PO_4\right)_2+3H_2\)
\(\Rightarrow\) \(F.\) \(H_3PO_4\) và \(G.\) \(H_2\) hhhhhhhh
\(\text{*)}\) Thừa thắng xông lên! Xét tiếp ở phương trình hóa học thứ năm với những công thức hóa học được tìm ra ở trên, nên dễ dàng xác định được CTHH của \(E\), ta có:
\(2H_2+O_2\) \(\rightarrow^{t^o}\) \(2H_2O\)
nên \(E.\) \(H_2O\)
\(\text{*)}\) Xong hiệp một rồi tiếp tay chém luôn hiệp hai, ta dễ dàng nhận ra phương trình hóa học thứ sáu giống với phương trình hóa học thứ nhất, ta có:
\(CaCO_3\) \(\rightarrow^{t^o}\) \(CO_2+CaO\) hoặc \(CaCO_3\) \(\rightarrow^{t^o}\) \(CaO+CO_2\)
nên xác định được \(I.\) \(CO_2\) và \(J.\) \(CaO\) hoặc \(I.\) \(CaO\) và \(J.\) \(CO_2\)
\(\text{*)}\) Ta có thể tìm ra CTHH \(J.\) thông qua phương trình hóa học cuối cùng với chú ý rằng \(K.\) làm đổi màu quỳ tím thành xanh. Khi đó, tìm ra được CTHH của \(I.\)
Xét hai trường hợp:
\(TH_1:\) Giả sử CTHH của \(J.\) là \(CaO\), phương trình cuối trở thành:
\(CaO+H_2O\) \(\rightarrow\) \(Ca\left(OH\right)_2\)
Vì \(Ca\left(OH\right)_2\) là dung dịch bazơ nên có thể làm quỳ tìm hóa màu xanh (t/mãn điều kiện)
\(TH_2:\) Giả sử CTHH của \(J.\) là \(CO_2\), phương trình cuối trở thành:
\(CO_2+H_2O\) \(\rightarrow\) \(H_2CO_3\)
Mà \(H_2CO_3\) làm đổi màu quỳ tìm thành đỏ (do là dung dịch axit) nên ta loại!
Vây, xác định \(K.\) có CTHH là \(Ca\left(OH\right)_2\)
\(\Rightarrow\) \(I.\) \(CO_2\) và \(J.\) \(CaO\)
Làm tương tự, ta tìm được CTHH của các chất còn lại!
\(A.\) \(O_2\)
\(B.\) \(KCl\)
\(C.\) \(P\)
\(D.\) \(P_2O_5\)
\(E.\) \(H_2O\)
\(F.\) \(H_3PO_4\)
\(G.\) \(H_2\)
\(I.\) \(CO_2\)
\(J.\) \(CaO\)
\(K.\) \(Ca\left(OH\right)_2\)
Bạn ghi lại tất cả PTHH nhé!

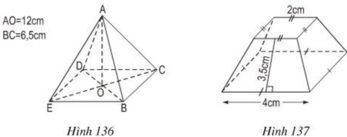
a) Diện tích đáy của hình chóp đều:
S = BC 2 = 6,52 = 42,25 (m2)
Thể tích hình chóp đều:
V = \(\dfrac{1}{3}\). S.h = \(\dfrac{1}{3}\). 42,25 . 12 ≈ 169 (cm3)
b) Các mặt xung quanh là những hình thang cân đáy nhỏ 2cm, đáy lớn 4cm, chiều cao 3,5cm. Nên:
Sxq = \(4.\dfrac{\left(2+4\right).3,5}{2}=42\left(cm^2\right)\) = 42 (cm2)