Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Bạn tự vẽ hình.
b) Hình minh họa :
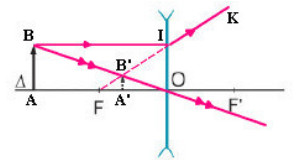
Xét \(\Delta FA'B'\sim\Delta FOI\) có : \(\dfrac{A'B'}{OI}=\dfrac{A'F}{OF}\Leftrightarrow\dfrac{A'B'}{AB}=\dfrac{OF-OA'}{OF}\)
\(\Rightarrow\dfrac{h'}{3}=\dfrac{15-d'}{15}\left(1\right)\)
Xét \(\Delta OA'B'\sim\Delta OAB\) có : \(\dfrac{A'B'}{AB}=\dfrac{OB'}{OB}\Leftrightarrow\dfrac{h'}{3}=\dfrac{d'}{30}\left(2\right)\).
Từ (1) và (2), ta có hệ phương trình : \(\left\{{}\begin{matrix}\dfrac{h'}{3}=\dfrac{15-d'}{15}\\\dfrac{h'}{3}=\dfrac{d'}{30}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}d'=10\left(cm\right)\\h'=1\left(cm\right)\end{matrix}\right.\).
Vậy : Ảnh A'B' cách thấu kính \(d'=10\left(cm\right)\) và cao \(h'=1\left(cm\right)\).


a)
O F F' A B B' A'
b)
Khoảng cách từ ảnh đến thấu kính là:
ADCT:\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Leftrightarrow d'=\dfrac{f.d}{f+d}=\dfrac{15.10}{15+10}=6\left(cm\right)\)
Chiều cao của ảnh là:
ADCT:\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow h'=\dfrac{h.d'}{d}=\dfrac{2.6}{10}=1.2\left(cm\right)\)
Vậy khoảng cách của ảnh đến thấu kính là 6(cm) và chiều cao của ảnh là 1,2(cm).
cần lắm rùi jup mh vs các bạn