Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi M(x,y) là 1 điểm thuộc (C) , M'(x';y') thuộc ảnh của (C) là ảnh của M qua phép tịnh tiến theo vecto u
=> \(\hept{\begin{cases}x'-x=-2\\y'-y=4\end{cases}}\Rightarrow\hept{\begin{cases}x=x'+2\\y=y'-4\end{cases}}\\ \)
thay x,y vào pt đường tròn (C)=> \(\left(x'+2\right)^2+\left(y'-4\right)^2-3\left(x'+2\right)+4\left(y'-4\right)-5=0\)
=> \(x'^2+4x'+4+y'^2-8y'+16-3x'-6+4y'-16-5=0\)
=>\(x'^2+x'+y'^2-4y'-7=0\)=>\(\left(x'+\frac{1}{2}\right)^2+\left(y'-2\right)^2=\frac{45}{4}\)

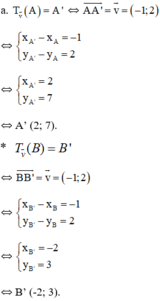
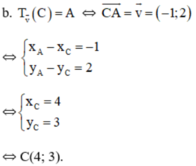
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0

a) Giả sử A'=(x'; y'). Khi đó \(T_{\overrightarrow{v}}\left(A\right)=A'\Leftrightarrow\left\{{}\begin{matrix}x'=3-1=2\\y'=5+2=7\end{matrix}\right.\)
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có: \(A=T_{\overrightarrow{v}}\left(C\right)\Leftrightarrow C=^T\overrightarrow{-v}\left(A\right)=\left(4;3\right)\)
c) Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = \(^T\overrightarrow{v}\) =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy \(^T\overrightarrow{v}\) (d) = d'.
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi \(^T\overrightarrow{v}\)(d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó \(^T\overrightarrow{v}\) (B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8.
a) Giả sử A'=(x'; y'). Khi đó
(A) = A' ⇔
Do đó: A' = (2;7)
Tương tự B' =(-2;3)
b) Ta có A = (C) ⇔ C=
(A) = (4;3)
c)Cách 1. Dùng biểu thức tọa độ của phép tịnh tiến
Gọi M(x;y), M' = =(x'; y'). Khi đó x' = x-1, y' = y + 2 hay x = x' +1, y= y' - 2. Ta có M ∈ d ⇔ x-2y +3 = 0 ⇔ (x'+1) - 2(y'-2)+3=0 ⇔ x' -2y' +8=0 ⇔ M' ∈ d' có phương trình x-2y+8=0. Vậy
(d) = d'
Cách 2. Dùng tính chất của phép tịnh tiến
Gọi (d) =d'. Khi đó d' song song hoặc trùng với d nên phương trình của nó có dạng x-2y+C=0. Lấy một điểm thuộc d chẳng hạn B(-1;1), khi đó
(B) = (-2;3) thuộc d' nên -2 -2.3 +C =0. Từ đó suy ra C = 8

a)
Qua phép đối xứng trục Oy điểm \(M\left(1;1\right)\) biến thành điểm \(M'\left(x;y\right)\) có tọa độ là: \(\left\{{}\begin{matrix}x'=-x=-1\\y'=y=1\end{matrix}\right.\).
Suy ra: \(M'\left(-1;1\right)\).
Qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\left(2;0\right)\) điểm M' biến thành điểm \(A\left(x_A;y_A\right)\) là:\(\left\{{}\begin{matrix}x_A=-1+2=1\\y_A=0+1=1\end{matrix}\right.\).
Suy ra: \(A\left(1;1\right)\equiv M\) là điểm cần tìm.
b) Gọi C là ảnh của điểm M qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\)
là: \(\left\{{}\begin{matrix}x_C=2+1=3\\y_C=0+1=1\end{matrix}\right.\). Suy ra: \(C\left(3;1\right)\)
\(M''=Đ_{Oy}\left(C\right)\) nên \(\left\{{}\begin{matrix}x_{M''}=-x_C=-3\\y_{M''}=y_C=1\end{matrix}\right.\). Suy ra: \(M''\left(-3;1\right)\).
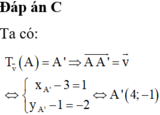
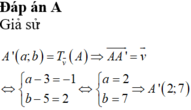
Đáp án B
Áp dụng biểu thức x ' = x + a y ' = y + b