Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Gọi số đó là \(\overline{ab}\)
a có 5 cách chọn (khác 0), b có 5 cách chọn (khác a)
Theo quy tắc nhân ta có: \(5.5=25\) số
b. Gọi số đó là \(\overline{abc}\)
a có 5 cách chọn (khác 0), b có 5 cách chọn (khác a), c có 4 cách chọn (khác a và b)
Có: \(5.5.4=100\) số
c. Gọi số đó là \(\overline{abcd}\)
Do số chẵn nên d chẵn
- TH1: \(d=0\) (1 cách chọn d)
a có 5 cách chọn (khác d), b có 4 cách chọn (khác a và d), c có 3 cách chọn
\(\Rightarrow1.5.4.3=60\) số
- TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (2 và 4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn (khác a và d), c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Theo quy tắc cộng, có: \(60+96=156\) số thỏa mãn
d.
Gọi số đó là \(\overline{abcde}\)
Số lẻ nên e lẻ \(\Rightarrow\) e có 3 cách chọn (1;3;5)
a có 4 cách chọn (khác 0 và e), b có 4 cách chọn (khác a và e), c có 3 cách, d có 2 cách
\(\Rightarrow3.4.4.3.2=288\) số
1.
Chữ số hàng đơn vị có 4 cách chọn (từ 1,3,5,7)
Chọn và hoán vị 4 chữ số từ 6 chữ số còn lại: \(A_6^4\) cách
Tổng cộng: \(4.A_6^4\) cách
2.
Gọi chữ số cần lập có dạng \(\overline{abcd}\)
a.
Lập số có 4 chữ số bất kì (các chữ số đôi một khác nhau): \(A_6^4\) cách
Lập số có 4 chữ số sao cho số 0 đứng đầu: \(A_5^3\) cách
\(\Rightarrow A_6^4-A_5^3=300\) số
b.
Để số được lập là số chẵn \(\Rightarrow\) d chẵn
TH1: \(d=0\Rightarrow abc\) có \(A_5^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (từ 2;4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn, c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Tổng cộng: \(A_5^3+96=156\) số
Xác suất \(P=\dfrac{156}{300}=...\)
Đáp án D
Phương pháp: Xét từng trường hợp: chữ số đầu tiên bằng 1, chữ số thứ hai bằng 1, chữ số thứ ba bằng 1.
Cách giải: Gọi số đó là a b c d e
- TH1: a = 1
+ b có 7 cách chọn.
+ c có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có: 7.6.5.4 = 840 số
- TH2: b = 1
+ a ≠ b , a ≠ 0 , nên có 6 cách chọn.
+ c có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có: 6.6.5.4 = 720 số.
- TH3: c = 1.
+ a ≠ c , a ≠ 0 , nên có 6 cách chọn.
+ b có 6 cách chọn.
+ d có 5 cách chọn.
+ e có 4 cách chọn.
Nên có 6.6.5.4 = 720 số.
Vậy có tất cả 840 + 720 + 720 = 2280 số.
Gọi số cần lập có dạng \(\overline{abcde}\)
e có 4 cách chọn (từ 1;3;5;7)
a có 6 cách chọn (khác 0 và e)
b có 6 cách chọn (khác a và e)
c có 5 cách chọn (khác a,b,e)
d có 4 cách chọn (khác a,b,c,e)
Theo quy tắc nhân, có: \(4.6.6.5.4=...\) số
Đáp án : D
Để tính nhanh với bài này ta dùng quy tắc phần bù.
Trước tiên ta tính số các số chẵn có 5 chữ số đôi một khác nhau và được lập ra từ các chữ số của tập A.
+ Gọi các số đó là 
e có 4 cách chọn( vì x là số chẵn nên e có thể là 2;34;6;8); a có 8 cách; b có 7 cách; c có 6 cách và d có 5 cách.
Nên có tất cả 4.8.7.6.5=6720 số
+ Gọi 
là số bắt đầu bởi 125 và có 5 chữ số đôi một khác nhau.
Suy ra b có 3 cách chọn (b có thể là 2;4;8), a có 5 cách chọn nên có số.
+ Suy ra có tất cả 6720 - 15 = 6705 số cần tìm.
Gọi 
là số cần lập .
Vì x là số chẵn nên e ∈ {0; ;2; 4; 6}. Ta xét các trường hợp sau
e = 0 ⇒ e có 1 cách chọn
Số cách chọn 
là một chỉnh hợp của 6 phần tử
Số cách chọn các chữ số còn lại là 
Do đó trường hợp này có tất cả 
số
e ≠ 0 ⇒ e có 3 cách chọn
Với mỗi cách chọn e ta có a ∈ A \ {0;e} nên có 5 cách chọn a.
Số cách chọn các số còn lại là: 
Do đó trường hợp này có tất cả 
số
Vậy có tất cả: 360 + 900 = 1260 số thỏa yêu cầu bài toán.
Chọn A.
Đáp án : A
+) 
; c có 4 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
+) 
; c có 3 cách chọn. Chọn chữ số còn lại có 7 cách chọn.
+) a = 7; 
; b khác 9, b có 6 cách chọn.
+) a = 7; c = 8; b có 6 cách chọn
Vậy có 3.4.7 + 3.3.7 + 3.6 + 6 = 171 số.
Lời giải:
Gọi số cần tìm có dạng $\overline{abc}$. Xét các TH sau:
TH1: $c=0$
$a$ có 7 cách chọn, từ $1,2,4,5,7,8,9$
$b$ có 6 cách chọn
$\Rightarrow$ có $7.6=42$ cách chọn số
TH2: $c\neq 0$
$c$ có 3 cách chọn $(2,4,8)$
$a$ có $6$ cách chọn (bỏ số 0)
$b$ có $6$ cách chọn
$\Rightarrow$ có $3.6.6=108$ cách chọn số
Từ 2 TH trên suy ra có $108+42=150$ cách chọn số.
Đáp án C.
Hướng dẫn giải: Gọi số cần tìm có dạng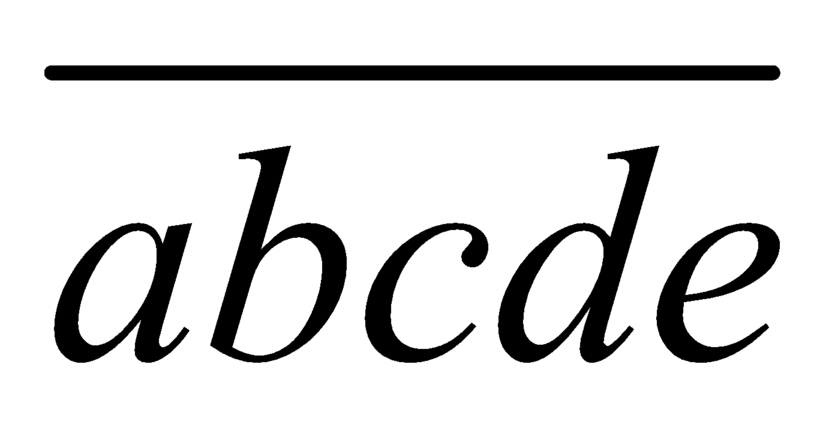
Chọn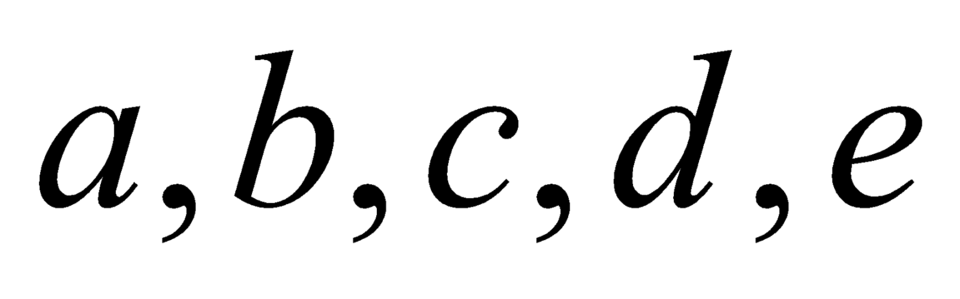
: có 
cách
Vậy c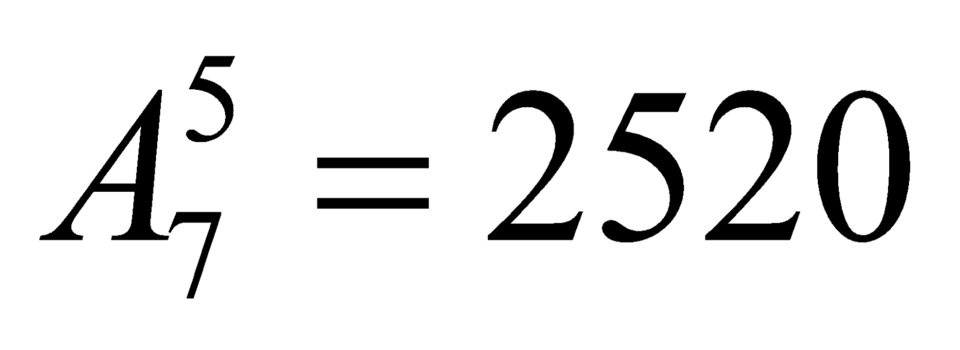ó
số.