Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tao có: \(\overrightarrow{BC}.\overrightarrow{AD}=\overrightarrow{BC}\left(\overrightarrow{DC}+\overrightarrow{CA}\right)=\overrightarrow{CB}.\overrightarrow{CD}-\overrightarrow{CB}.\overrightarrow{CA}\)
\(=\frac{1}{2}\left(CB^2+CD^2-BD^2\right)-\frac{1}{2}\left(CB^2+CA^2-AB^2\right)\)
\(=\frac{1}{2}\left(AB^2+CD^2-BD^2-CA^2\right)\)
\(\Rightarrow\cos\left(\overrightarrow{BC},\overrightarrow{DA}\right)=\frac{1}{2}.\frac{c^2+c'^2-b^2-b'^2}{2aa'}\)

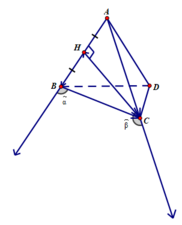
Tứ diện ABCD đều có các mặt là tam giác đều
a) Góc giữa A B → v à B C → là góc α ^ và
α ^ = 180 o - 60 o = 120 o
b) Góc giữa C H → v à A C → là β ^
H là trung điểm cạnh AB của tam giác đều ABC nên CH vừa là trung tuyến vừa là đường cao nên CH ⊥ AB
Xét tam giác vuông ACH tại H có
A C H ^ + H A C ^ = 90 o ⇒ A C H ^ = 90 o - 60 o = 30 o
Nên β ^ = 180 o - 30 o = 150 o

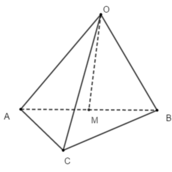
Tam giác OAB vuông tại O (OA ⊥ OB)
Theo định lý Py-ta-go ta có: A B = O A 2 + O B 2 = 1 2 + 1 2 = 2
Tương tự BC = 2
Ta có: OM là trung tuyến của tam giác OAB vuông tại O
Nên OM = 1/2AB = 1 2 . 2 = 2 2
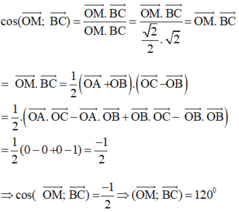
Đáp án D

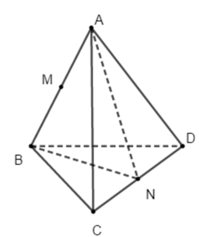
Các tam giác ABC và ABD là tam giác đều ⇒ tam giác ACD cân
⇒ BN ⊥ CD và AN ⊥ CD ⇒ góc ANB là góc của hai mặt phẳng (ACD) và (BCD)
Đáp án B

Gọi d = 2a là công sai. Bốn số phải tìm là \(A=\left(x-3a\right);B=\left(x-a\right);C=\left(x+a\right);D=\left(x+3a\right)\)
Ta có hệ phương trình :
\(\begin{cases}\left(x-3a\right)+\left(x-a\right)+\left(x+a\right)+\left(x+3a\right)=360^0\\\left(x+3a\right)=5\left(x-3a\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}x=90^0\\a=20^0\end{cases}\)
Bốn góc phải tìm là : \(A=30^0;B=70^0;C=110^0;D=150^0\)

Lấy điểm N sao cho tứ giác CDMN là hình bình hành => ∠CNM=∠CDM=∠CBM
Ta có:\(\overrightarrow{AB}=\overrightarrow{DM}=\overrightarrow{CN}\)
Tứ giác BMCN có ∠CNM=∠CBM nên là tứ giác nội tiếp
(1) và (2)=> ∠ACD=∠BCM