Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

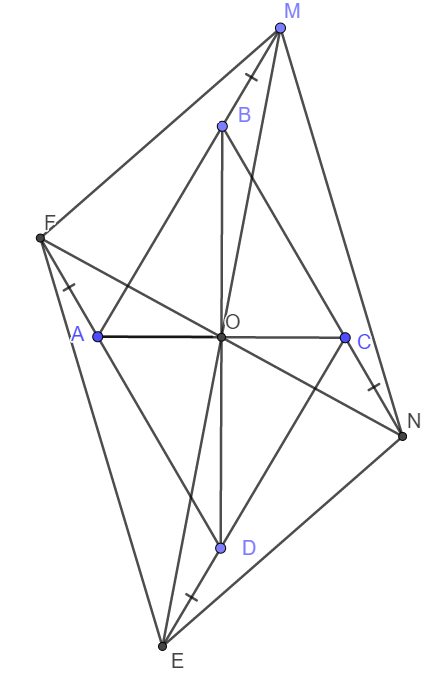
a) Do ABCD là hình thoi nên \(\widehat{BAD}=\widehat{DCB}\)
Suy ra \(\widehat{FAM}=\widehat{NCE}\)
Cũng do ABCD là hình thoi nên AB = CD, hay AM = CE
Xét tam giác FAM và tam giác NCE có:
FA = NC
AM = CE
\(\widehat{FAM}=\widehat{NCE}\)
\(\Rightarrow\Delta FAM=\Delta NCE\left(c-g-c\right)\)
b) Từ câu a ta có: FM = NE
Chứng minh tương tự câu a thì \(\Delta EDF=\Delta MBN\left(c-g-c\right)\Rightarrow FE=NM\)
Xét tứ giác MNEF có FM = NE, FE = MN nên MNEF là hình bình hành.
c) Gọi O là giao điểm của AC và BD. Do ABCD là hình thoi nên O là trung điểm AC và BD.
Xét tứ giác AFCN có FA song song và bằng CN nên AFCN là hình bình hành.
Suy ra FN cắt AC tại trung điểm mỗi đường. Suy ra O là trung điểm FN.
Tương tự BMDE là hình bình hành nên O là trung điểm ME.
Tóm lại O là trung điểm của FN và ME hay O là giao điểm hai đường chéo của cả hình bình hành MNEF và hình thoi ABCD.
bài c mk có cách giải kc rùi nhưng cx cảm ơn bk và mk k cho bạn


a. Xét tam giác HCD cóHN=DN;HM=CM
=> MN là đường trung bình của tam giác HCD => MN//DC
=> DNMC là hình thang
b. Ta có MN là đường trung bình của tam giác HCD => MN=1/2CD
Mà AB=1/2CD => AB =MN
Do MN//CD và AB//CD => AB//MN
Xét tứ giác ABMN có AB//MN; AB=MN
=> ABMN là hình bình hành
c.Ta có MN//CD mà CD vg AD
=> MN vg AD
Xét tam giác ADM có DH và MN là 2 đường cao của tam giác
Mà chúng cắt nhau tại N nên N là trực tâm của tam giác ADM
=> AN là đường cao của tam giác ADM
=> AN vg DM
Do ABMN là hình bình hành nên AN//BM
=> BM vg DM => BMD =90*

gọi độ dài cạnh hình tam giác là a.
áp dụng công thức S=\(\frac{a^2\cdot\sqrt{3}}{4}\)=121\(\sqrt{3}\)
bạn tự tính tiếp nha!!!!!!!!!!!!!