Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1
Trong tam giác ADC, E là trung điểm của AD, I là trung điểm của AC nên EI là đường trung bình
Suy ra EI //CD Hay EI =1/2CD
Trong tam giác ABC, F là trung điểm của BC, I là trung điểm của AC nên FI là đường trung bình
Suy ra FI //AB Hay FI=1/2AB
Câu 2
Trong tam giác EIF thì:
EF < EI+IF
EF < 1/2CD +1/2AB
EF < 1/2(AB+CD)
A B D C E F I

Gọi K là trung điểm của AC .
Xét tam giác ADC ta có :
\(AE=DE\)(GT)
\(AK=CK\)(GT)
=> EK là đường trung bình của tam giác ADC
\(\Rightarrow EK=\frac{1}{2}CD\)
Xét tam giác ABC ta có :
\(BF=CF\)(GT)
\(KA=KC\)(GT)
=> KF là đường trung bình của tam giác ABC
+) Xét tam giác EFK ta có :
\(EF\le EK+KF\)
Mà \(EK=\frac{1}{2}CD\)( chứng minh trên )
\(KF=\frac{1}{2}AB\)( chứng minh trên )
\(\Rightarrow EK+KF=\frac{CD}{2}+\frac{AB}{2}\)
\(=\frac{AB+CD}{2}\)
Vậy \(EF\le\frac{AB+CD}{2}\) ( đpcm)

A B C D E F K
a) +)EK là đường trung bình nên EK = 1/2 . CD do đó EK < CD
+) EF và AB thì đang suy nghĩ
b) Ta có: \(EK=\frac{1}{2}CD=\frac{CD}{2}\)(t/c đường trung bình)
Tương tự, ta có \(KF=\frac{1}{2}AB\)
Cộng theo vế hai đẳng thức trên ta được:
\(\frac{AB+CD}{2}=EK+KF\ge EF\) ( theo quy tắc 3 điểm)
Đẳng thức xảy ra khi K thuộc EF, khi đó \(\hept{\begin{cases}EK\text{// }CD\\KF\text{//}AB\end{cases}}\) và K thuộc EF nên suy ra \(\hept{\begin{cases}EF\text{//}CD\\EF\text{//}AB\end{cases}}\Leftrightarrow AB\text{//}CD\)
P/s: Chỗ "đẳng thức xảy ra..." mình không chắc.

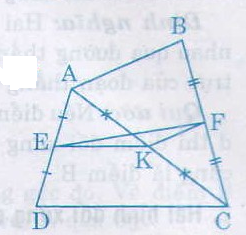
a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK = CD/2
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = AB/2
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = CD/2 + AB/2 = (AB+CD)/2
Vậy EF ≤ (AB+CD)/2
27. Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.
a) So sánh các độ dài EK và CD, KF và AB.
b) Chứng minh rằng EF \(\le\dfrac{AB+CD}{2}\)
Bài giải:

a) Trong ∆ACD có EA = ED, KA = KC (gt)
nên EK là đường trung bình của ∆ACD
Do đó EK =\(\dfrac{CD}{2}\)
Tương tự KF là đường trung bình của ∆ABC.
Nên KF = \(\dfrac{AB}{2}\)
b) Ta có EF ≤ EK + KF (bất đẳng thức trong ∆EFK)
Nên EF ≤ EK + KF = \(\dfrac{CD}{2}\) + \(\dfrac{AB}{2}\) = \(\dfrac{\left(AB+CD\right)}{2}\)
Vậy EF ≤ \(\dfrac{\left(AB+CD\right)}{2}\)

Ta có hình vẽ: A B C D E F I
a) Xét \(\Delta ADC\) có:
AE = ED (gt)
AI = IC (gt)
=> EI là đường trung bình
=> EI // DC
Xét \(\Delta CAB\) có:
AI = IC (gt)
BF = FC (gt)
=> IF là đường trung bình
=> IF // AB
b) Ta có: EF \(\le\) EI + IF
mà IF + EF = \(\dfrac{1}{2}\) AB + \(\dfrac{1}{2}\) CD
= \(\dfrac{1}{2}\) (AB + CD)
=> EF \(\le\) \(\dfrac{\left(AB+CD\right)}{2}\) (đpcm)

a: Xét ΔADC có
E là trung điểm của AD
K là trung điểm của AC
DO đó: EK là đường trung bình
=>EK//CD và EK=CD/2
b: Xét ΔCAB có
Flà trung điểm của CB
K là trung điểm của CA
Do đó FK là đường trung bình
=>FK//AB và FK=AB/2
EF<=EK+KF
nên EF<=1/2(AB+CD)
c:Khi EF=1/2(AB+CD) thì EF=EK+KF
=>E,K,F thẳng hàng
=>AB//CD
hay ABCD là hình thang
