Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

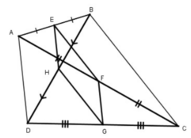
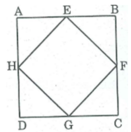
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình vuông khi và chỉ khi EFGH là hình chữ nhật đồng thời là hình thoi
⇔ AD ⊥ BC và AD = BC
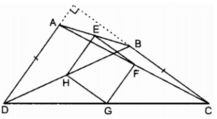

Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AD ⊥ BC
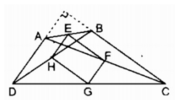

* Ta có EF là đường trung bình của ∆ ABC
Suy ra: EF //AC và EF = 1/2 AC (1)
* Trong ∆ ADC có HG là đường trung bình
Suy ra: HG // AC và HG = 1/2 AC (2)
Từ (l) và (2) suy ra EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành.
Tứ giác EFGH là hình thoi ⇔ EH = EF ⇔ AC = BD

a: Xét ΔBAD có
E là tđiểm của AB
H là tđiểm của BD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//AD và EH=AD/2(1)
Xét ΔACD có
F là trung điểm của AC
G là trung điểm của CD
Do đó: FG là đường trung bình của ΔACD
Suy ra: FG//AD và FG=AD/2(2)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EFGH là hình bình hành

Cái hình hơi khó vẽ! :(
Giải:
Ta có: \(EA=EB,FB=FC\left(gt\right)\)
\(\Rightarrow EF\) là đường trung bình của \(\Delta BAC\)
\(\Rightarrow\) \(EF//AC\) và \(EF=\dfrac{AC}{2}\left(1\right)\)
Chứng minh tương tự ta có:
\(HG//AC\) và \(HC=\dfrac{AC}{2}\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) suy ra: \(EF//GH\) và \(EF=GH\)
\(\Rightarrow EFGH\) là hình bình hành
a) Hình bình hành \(EFGH\) là hình chữ nhật
\(\Leftrightarrow\widehat{FEH}=90^0\Leftrightarrow EF\perp EH\Leftrightarrow AC\perp BD\)\((EF//AC,EH//BD)\)
b) Hình bình hành \(EFGH\) là hình thoi
\(\Leftrightarrow EF=EH\Leftrightarrow AC=BD\) \(\left(EF=\dfrac{AC}{2};EH=\dfrac{BD}{2}\right)\)
c) Hình bình hành \(EFGH\) là hình vuông \(\Leftrightarrow\left\{{}\begin{matrix}AC\perp BD\\AC=BD\end{matrix}\right.\)

Chứng minh EFGH là hình bình hành. Để EFGH là hình chữ nhật thì
Þ H E F ^ = 90 0 ⇒ H E ⊥ E F
Þ AC ^BD.
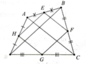

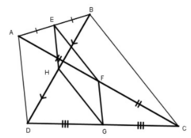
Xét tam giác ABC:
Ta có: EB = EA, FA = FC (gt)
Nên EF là đường trung bình của tam giác ABC
Nên EF // BC, EF = 1/2 BC.
Xét tam giác BDC có
HB = HD, GD = GC (gt)
Nên HG là đường trung bình của tam giác BDC
Nên HG // BC, HG = 1/2 BC.
Do đó EF //HG, EF = HG.
Tương tự EH // FG, EH = FG
Vậy EFGH là hình bình hành.
EFGH là hình thoi ⇔ EH = EF ⇔ AD = BC