Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì ABCD là hình bình hành\(\Rightarrow AB//CD\)
mà \(E\in CD,F\in CD\)\(\Rightarrow AE//DF,BE//CF\left(đpcm\right)\)
b) ABCD là hình bình hành \(\Rightarrow AB=CD\)
mà \(AE=DF\left(gt\right)\)\(\Rightarrow BE=CF\left(đpcm\right)\)
c) Tứ giác AEFD có AE // DF, AE = DF
\(\Rightarrow\)Tứ giác AEFD là hình bình hành (đpcm)
d) Chứng minh tương tự phần c ta suy ra đpcm

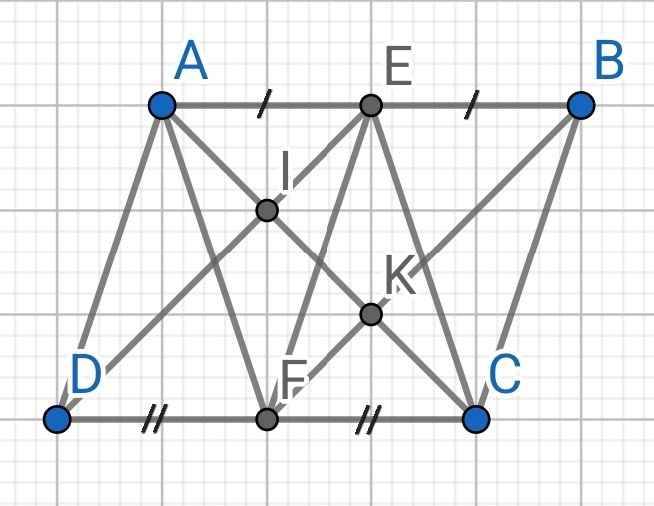 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: Xétbtứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
mà AM=AD
nên AMND là hình thoi
c: Xét ΔANQ có
AD là đường trung tuyến
AD=QN/2
Do đó: ΔANQ vuông tại A
Xét tứ giác ANKQ có
D là trung điểm của AK
D là trung điểm của NQ
Do đó; ANKQ là hình bình hành
mà \(\widehat{NAQ}=90^0\)
nên ANKQ là hình chữ nhật

a) Xét ΔABD có
H là trung điểm AD
E là trung điểm AB
=> HE là đường trung bình ΔABD
=> HE//BD và HE = 1/2 BD (1)
CMTT => GF // BD và GF = 1/2 BD (2)
Từ (1) và (2) => HEFG là hình bình hành.
b) Để EFGH là hình chữ nhật
<=> HE = HG. Mà HE = 1/2 BD
HG = 1/2 AC
<=> BD = AC
Vậy khi hai đường chéo AC và BD của tứ giác ABCD bằng nhau thì EFGH là hình chữ nhật.

b: Xét tứ giác MCNA có
MC//NA
MC=NA
Do đó: MCNA là hình bình hành
Suy ra: MA//NC và MA=NC(2)
hay MP//NQ(1)
Xét tứ giác BMNA có
BM//NA
BM=NA
Do đó: BMNA là hình bình hành
Suy ra: BN và MA cắt nhau tại trung điểm của mỗi đường
hay P là trung điểm của MA
=>PM=MA/2(3)
Xét tứ giác MCDN có
MC//DN
MC=DN
Do đó: MCDN là hình bình hành
Suy ra: MD và CN cắt nhau tại trung điểm của mỗi đường
=>Q là trung điểm của CN
=>NQ=CN/2(4)
Từ (2), (3) và (4) suy ra MP//NQ(5)
Từ (1) và (5) suy ra MPNQ là hình bình hành(6)
Xét hình bình hành BMNA có BM=BA
nên BMNA là hình thoi
=>BN⊥MA
hay \(\widehat{MPN}=90^0\)(7)
Từ (6) và (7) suy ra PMQN là hình chữ nhật
c: Để hình chữ nhật PMQN là hình vuông thì MP=PN
=>BN=MA
=>BMNA là hình vuông
=>\(\widehat{ABC}=90^0\)
ai tra loi nhanh cau hoi nay ho minh voi minh k cho
ai tra loi nhanh cau hoi nay ho minh voi minh k cho