Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABD có AE/AB=AH/AD
nên EH//BD và EH=BD/2
Xet ΔCBD có CF/CB=CG/CD
nên FG//BD và FG=BD/2
=>EH//FG và EH=FG
Xét ΔBAC có BE/BA=BF/BC
nên EF//AC
=>EF vuông góc BD
=>EF vuông góc EH
=>EFGH là hình chữ nhật
=>E,F,G,H cùng thuộc 1 đường tròn
=>Bán kính là R=EG/2

Do ABCD là hình thoi \(\Rightarrow\Delta BCD\) cân tại C
Mà \(C=60^0\Rightarrow\Delta BCD\) đều
Hoàn toàn tương tự, ta có tam giác ABD đều
\(\Rightarrow AB=BC=CD=DA=BD\) (1)
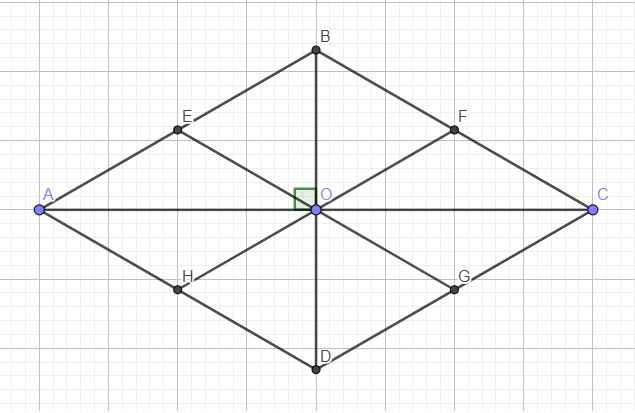
Gọi O là giao điểm 2 đường chéo \(\Rightarrow OA\perp OB\)
Trong tam giác vuông OAB, do E là trung điểm AB nên OE là trung tuyến ứng với cạnh huyền
\(\Rightarrow OE=\dfrac{1}{2}AB\) (2)
Mà O là trung điểm BD (tính chất hình thoi) \(\Rightarrow OB=\dfrac{1}{2}BD\) (3)
(1);(2);(3) \(\Rightarrow OE=OB\)
Hoàn toàn tương tự, ta có:
\(OE=OB=OF=OG=OD=OH\)
\(\Rightarrow\) Các điểm E, B, F, G, D, H cùng thuộc 1 đường tròn tâm O bán kính OB

Xét ΔABD có AB=AD và góc BAD=60 độ
nên ΔABD đều
Ta có: ΔDAB cân tại D
mà DE là đường trung tuyến
nên DE vuông góc với BE
=>E nằm trên đường tròn đường kính BD(1)
Ta có:ΔBAD cân tại B
ma BH là đường trung tuyến
nên BH vuông góc với HD
=>H nằm trên đường tròn đường kính BD(2)
Xét ΔCBD có CB=CD và góc BCD=60 độ
nên ΔCBD đều
Ta có: ΔBDC cân tại D
mà DF là đường trung tuyến
nen DF vuông góc với BF
=>F nằm trên đường tròn đường kính BD(3)
Ta có: ΔBDC cân tại B
mà BG là đường trung tuyến
nên BG vuông góc với GD
=>G nằm trên đường tròn đường kính BD(4)
Từ (1), (2), (3) và (4) suy ra E,B,F,G,D,H cùng nằm trên 1 đường tròn