Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình lm tắt bạn tự hiểu nhé, ko hiểu chỗ nào thì hỏi mik
tam giác ADC= tam giác ABC (c.c.c)
=> A1=A2 (2 góc tg ứng)
=> AC là p/giác tam giác ADB (1)
Mà tam giác ABD cân do AD= AB ( giả thiết) (2)
từ (1) và (2) => AC là trung trực tam giác ADB
=> AClà trung trực BD (đpcm)
còn tính cái kia thì bạn lm theo hướng như sau
Vì tam giác ADC = tam giác ABC (cmt)
=> C1=C2= góc DCB :2 = 60 độ :2 = 30 độ
Còn A1=A2(cmt) => A1=A2=góc DAB:2 = 120 độ :2 = 60 độ
Xét tam giác ABC có tổng 3 góc = 180 độ r trừ đi góc A2 và góc C2 vừa tìm ra góc B= 90 độ
Vì tam giác ADC = tam giác ABC (cmt)
=> góc B= góc D ( 2 góc tg ứng) => góc D= 90 độ
Vậy D=B=90 độ

a: Ta có: BA=BC
DA=DC
Do đó:BD là đường trung trực của AC
b: Đặt góc A=a; góc B=b; góc C=c; góc D=d
Xét ΔBAD và ΔBCD có
BA=BC
AD=CD
BD chung
Do đó:ΔBAD=ΔBCD
Suy ra: góc BAD=góc BCD
hay a=c
b-d=10 nên d=b-10
a-b=21 nên a=b+21
c=a nên c=b+21
Xét tứ giác ABCD có góc A+góc B+góc C+góc D=360
=>a+b+c+d=360
=>b-10+b+21+b+21+b=360
=>4b+32=360
=>4b=328
hay b=82
=>a=c=b+21=103 độ
d=b-10=72

Tự vẽ hình nha
a) Có : AB=AD(gt)
=> A\(\in\)đường trung trực của đoạn thẳng BD(1)
Có: CB=CD(gt)
=> C\(\in\)đường trung trực của đoạn thẳng BD(2)
Từ 1,2 suy ra:
A,C \(\in\)Đường trung trực của đoạn thẳng BD
=> AC là đường trung trực của đoạn thẳng BD
b, Xét tam giác ABC và ADC có:
AB=AD(gt)
BC=DC(gt)
AC: góc chung
=> tam giác ABC=ADC( c.c.c)
=> ^BAC=^DAC(2 góc tương ứng)
^BCA=^DCA(2 góc tương ứng)
^ABC=^ADC(2 góc tương ứng)
Có: ^BAD=^BAC+^DAC=100
=> ^BAC=^DAC=50
Lại có ^BCD=^BAC+^DCA=60
=> ^BAC=^DCA=30
Xét tam giác ABC có: ^BAC+^ACB+^ABC=180
=> ^ABC=180- ^ACB - ^BAC=180 -60-100=20
Vậy ^B = ^C = 20
Tích mink nha (^.^)

a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ \(\widehat{B}=\widehat{D}\)
Ta có \(\widehat{B}+\widehat{D}=360^o-\left(100^o+60^o\right)=200^o\)
Do đó \(\widehat{B}=\widehat{D}=100^o\)
Bài giải:
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ˆB=ˆD⇒B^=D^
Ta có ˆB+ˆD=3600−(100+60)=200B^+D^=3600−(100+60)=200
Do đó ˆB=ˆD=1000B^=D^=1000

Trên cạnh AD bạn lấy điểm E sao cho AE = AB => hai tam giác ACE và ACB bằng nhau (c.g.c)
=> CE = CB (1)
và góc AEC = ABC = 110 độ.
xét tam giác CED có D = 70 độ
theo tính chất góc ngoài AEC = tổng hai góc trong không kề nó. Bạn dễ dàng tính được ECD = 40 độ.
Từ đó có được góc CED = 70 độ
Suy ra tam giác CED cân tại C , tức là CE = CD (2)
Từ (1) và (2) => đpcm

Bài 1)
Trên AD lấy E sao cho AE = AB
Xét ∆ACE và ∆ACB ta có :
AC chung
DAC = BAC ( AC là phân giác)
AB = AE (gt)
=> ∆ACE = ∆ACB (c.g.c)
=> CE = CB (1)
=> AEC = ABC = 110°
Mà AEC là góc ngoài trong ∆EDC
=> AEC = EDC + ECD ( Góc ngoài ∆ bằng tổng 2 góc trong không kề với nó)
=> ECD = 110 - 70
=> EDC = 40°
Xét ∆ EDC :
DEC + EDC + ECD = 180 °
=> CED = 180 - 70 - 40
=> CED = 70°
=> CED = EDC = 70°
=> ∆EDC cân tại C
=> CE = CD (2)
Từ (1) và (2) :
=> CB = CD (dpcm)
b) Ta có thể thay sao cho tổng 2 góc đối trong hình thang phải = 180°

a) HS tự chứng minh
b) Sử dụng tổng bốn góc trong tứ giác và chú ý B ^ = D ^
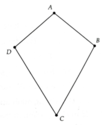

Mình lm tắt bạn tự hiểu nhé, ko hiểu chỗ nào thì hỏi mik
tam giác ADC= tam giác ABC (c.c.c)
=> A1=A2 (2 góc tg ứng)
=> AC là p/giác tam giác ADB (1)
Mà tam giác ABD cân do AD= AB ( giả thiết) (2)
từ (1) và (2) => AC là trung trực tam giác ADB
=> AClà trung trực BD (đpcm)