Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Vẽ ∆DBC biết BD = 5 cm, BC = 10 cm, DC = 12,5 cm.
Trên nửa mặt phẳng bờ BD không chứa C vẽ hai cung tròn tâm B và tâm D bán kính lần lượt là 4 cm và 8 cm. Hai cung này cắt nhau tại A.
Vẽ các đoạn BA, DA được tứ giác ABCD.
ABBD=410=25;BDDC=1025=25;ADBC=820=25ABBD=410=25;BDDC=1025=25;ADBC=820=25
=>ABBD=BDDC=ADBC=>ΔABDΔBDCABBD=BDDC=ADBC=>ΔABDΔBDC
∆ABD∽ ∆BDC =>ˆABD=ˆBDCABD^=BDC^ lại so le trong.
=>AB // DC hay ABCD là hình thang.


Chứng minh △ ABD ∼ △ BDC (c.c.c)
⇒ ∠ (ABD) = ∠ (BDC) ⇒ AB // CD.

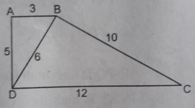
a: Xét ΔABD và ΔBDC có
\(\dfrac{AB}{BD}=\dfrac{BD}{DC}=\dfrac{AD}{BC}\left(\dfrac{3}{6}=\dfrac{6}{12}=\dfrac{5}{10}\right)\)
Do đó: ΔABD~ΔBDC
b: Ta có: ΔABD~ΔBDC
=>\(\widehat{ABD}=\widehat{BDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
=>ABCD là hình thang

a) Gợi ý: Lập tỉ số các cặp cạnh tương ứng và chứng minh chúng bằng nhau.
b) Từ phần a 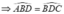 Þ ĐPCM
Þ ĐPCM

a: Xét ΔABD và ΔBDC có
AB/BD=BD/CD=AD/BC
=>ΔABD đồng dạng với ΔBDC
b: ΔABD đồng dạng với ΔBDC
=>góc ABD=góc BDC
=>AB//CD
Chung minh ABD đồng dạng với BDC
=> \(\widehat{ABD}\)=\(\widehat{BDC}\)
hai góc này ở vị trí sole trong
=> AB//CD