Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B C A D E F G H
a) Xét \(\Delta ADC\) có :
\(AF=FC\left(gt\right)\)
\(AG=CD\left(gt\right)\)
=> \(FG\) là đường trung bình của \(\Delta ADC\)
=> \(\left\{{}\begin{matrix}\text{FG//DC}\\FG=\dfrac{1}{2}DC\end{matrix}\right.\) (tính chất đường trung bình trong tam giác) (1)
Xét \(\Delta BDC\) có :
\(BE=EC\left(gt\right)\)
\(BH=HD\left(gt\right)\)
=> \(EH\) là đường trung bình của \(\Delta BDC\)
=> \(\left\{{}\begin{matrix}\text{EH//DC}\\EH=\dfrac{1}{2}DC\end{matrix}\right.\)(tính chất đường trung bình trong tam giác) (2)
Từ (1) và (2) => \(\left\{{}\begin{matrix}\text{FG//EH}\\FG=EH\end{matrix}\right.\)
=> Tứ giác EFGH là hình bình hành
Có thêm : \(AB\perp CD\left(gt\right)\)
Mà : \(\text{EH // CD (cmt)}\)
=> \(EH\perp AB\)
Xét \(\Delta ABC\) có :
\(BE=EC\left(gt\right)\)
\(AF=FC\left(gt\right)\)
=> EF là đường trung bình trong tam giác ABC
=> \(\text{EF // AB }\)
Ta thấy : \(\text{EF // AB }\left(cmt\right)\)
Mà : \(EH\perp AB\left(cmt\right)\)
=> \(EF\perp EH\)
=> Tứ giác EFGH là hình chữ nhật
=> \(EG=FH\) (2 đường chéo trong hình chữ nhật)
b) Để \(\text{ BC // AC }\) thì :
\(\Leftrightarrow\) Tứ giác ABCD là hình thang

+ Xét tg BCD có EF là đường trung bình => EF//=CD/2
+ Xét tg ACD có GH là đường trung bình => GH//=CD/2
=> EF//=GH => EFGH là hình bình hành (1)
+ Xét tg ABC có HE là đường trung bình => HE=AB/2 mà EF=CD/2 và AB=CD => EF=HE (2)
Từ 91) và (2) => EFGH là hình thoi => EG vuông góc với FH (2 đường chéo của hình thoi vuông góc với nhau)

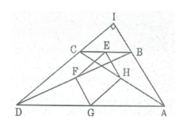
* Trong ∆ BCD, ta có:
E là trung điểm của BC (gt)
F là trung điểm của BD (gt)
Suy ra EF là đường trung bình của ∆ BCD
⇒ EF // CD và EF = 1/2 CD (1)
* Trong ∆ ACD, ta có: H là trung điểm của AC (gt)
G là trung điểm của AD (gt)
Suy ra HG là đường trung bình của ∆ ACD
⇒HG // CD và HG = 1/2 CD (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
* Mặt khác: EF // CD (chứng minh trên)
AB ⊥ CD (gt)
Suy ra EF ⊥ AB
Trong ∆ ABC ta có HE là đường trung bình ⇒ HE // AB
Suy ra: HE ⊥ EF hay ∠ (FEH) = 90 0
Vậy hình bình hành EFGH là hình chữ nhật.