

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



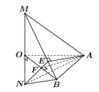
Do tam giác OAB đều cạnh a suy ra F là trung điểm OB => O F = a 2
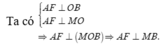
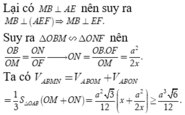
Đẳng thức xảy ra khi và chỉ khi ![]()
Chọn B.

Đáp án C
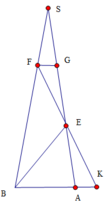
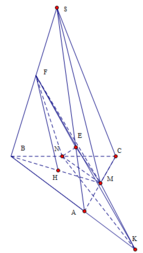
Ta có ∆ A B C vuông cân tại B nên M là tâm đường tròn ngoại tiếp. S M = S B = S C ⇒ S M ⊥ ( A B C )
F E ∩ A B = K , kẻ F G / / B A F H / / S M ⇒ F H ⊥ ( A B C ) ta có: F H = 2 3 S M = 2 3 S A 2 - A M 2 = 2 3 12 2 - 8 = 4 3 34
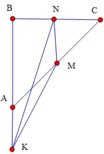
d t K M N = d t B N M K - d t B N K = 1 2 ( M N + B K ) . B N - 1 2 M N . B N = 1 2 . 2 . 2 = 2
∆ F G E = ∆ K A E ( C . G . C ) ⇒ F E = 1 2 F K
V F M N E V F M N K = F E F K = 1 2 ⇒ V F M N E = 1 2 V F M N K = 1 2 . 1 3 . F H . d t K M N = 1 6 . 4 3 34 . 2 = 4 34 9

a: Xét tứ giác ABDE có
M là trung điểm của AD
M là trung điểm của BE
Do đó: ABDE là hình bình hành
Suy ra: AE=BD
b: Xét tứ giác AFDC có
M là trung điểm của AD
M là trung điểm của CF
Do dó: AFDC là hình bình hành
Suy ra: FA//DC
hay FA//BC
c: Ta có: AF//BC
AE//BC
mà AE,AF có điểm chung là A
nên A,E,F thẳng hàng

Đáp án B

Ta có
A F ⊥ O B , A F ⊥ M O ⇒ A F ⊥ M O B ⇒ A F ⊥ M B
Mà M B ⊥ A E nên M B ⊥ A E F ⇒ M B ⊥ E F .
Suy ra Δ M O B ∽ Δ M E N , mà Δ M E N ∽ Δ F O N nên Δ M O B ∽ Δ F O N . Khi đó O B O M = O N O F ⇒ O N = O B . O F O M = a . a 2 x = a 2 2 x .
Từ
V A B M N = V M . O A B + V N . O A B = 1 3 . S Δ O A B . O M + O N = 1 3 . a 2 3 4 . x + a 2 2 x
⇒ V A B M N = a 2 3 12 x + a 2 2 x ≥ a 2 3 12 .2 x . a 2 2 x = a 2 3 12 . 2 a = a 3 6 12
Dấu “=” xảy ra
⇔ x = a 2 2 x ⇔ 2 x 2 = a 2 ⇔ x = a 2 2 .

Chọn A
Xét một trường hợp đặc biệt của các điểm M, E, F ta tính được T = 1.