Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

TenAnh1 TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) E = (-3.34, -5.86) E = (-3.34, -5.86) E = (-3.34, -5.86) F = (12.02, -5.86) F = (12.02, -5.86) F = (12.02, -5.86) G = (-3.7, -5.88) G = (-3.7, -5.88) G = (-3.7, -5.88) H = (11.66, -5.88) H = (11.66, -5.88) H = (11.66, -5.88) I = (-3.74, -5.62) I = (-3.74, -5.62) I = (-3.74, -5.62) J = (11.62, -5.62) J = (11.62, -5.62) J = (11.62, -5.62) A'

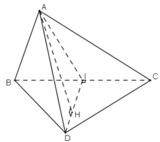
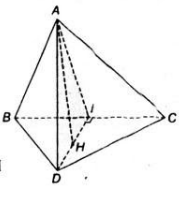
a) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao:
AI ⊥ BC
+) Tương tự, tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao:
DI ⊥ BC
+) Ta có: 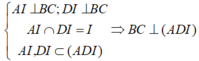
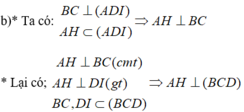

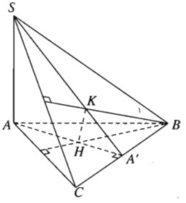
a) Gọi A’ là giao điểm của AH và BC. Ta cần chứng minh ba điểm S, K, A’ thẳng hàng.
Vì H là trực tâm của tam giác ABC nên AA′ ⊥ BC. Mặt khác theo giả thiết ta có: SA ⊥ (ABC), do đó SA ⊥ BC.
Từ đó ta suy ra BC ⊥ (SAA′) và BC ⊥ SA′. Vậy SA’ là đường cao của tam giác SBC nên SA’ là phải đi qua trực tâm K. Vậy ba đường thẳng AH, SK và BC đồng quy.
b) Vì K là trực tâm của tam giác SBC nên BK ⊥ SC (1)
Mặt khác ta có BH ⊥ AC vì H là trực tâm của tam giác ABC và BH ⊥ SA vì SA ⊥ (ABC).
Do đó BH ⊥ (ABC) nên BH ⊥ SC (2).
Từ (1) và (2) ta suy ra SC ⊥ (BHK). Vì mặt phẳng (SAC) chứa SC mà SC ⊥ (BHK) nên ta có (SAC) ⊥ (BHK).
c) Ta có
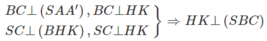
Mặt phẳng (BHK) chứa HK mà HK ⊥ (SBC) nên (BHK) ⊥ (SBC).

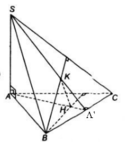
1) Ta có : \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
BC \(\perp AB;BC\perp SA\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) \(\Rightarrow\Delta SBC\perp\) tại B
2) \(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) . Mà
\(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp HK\) \(\Rightarrow\Delta AHK\perp\) tại H
\(\Delta SAB\perp\) tại A ; \(AH\perp SB\) có : \(AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a^2}{\sqrt{2a^2}}=\dfrac{\sqrt{2}}{2}a\)
AC = \(\sqrt{AB^2+BC^2}=\sqrt{2a^2}=\sqrt{2}a\)
\(\Delta SAC\perp\) tại A có : \(AK\perp SC\) có :
\(AK=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a.\sqrt{2}a}{\sqrt{a^2+2a^2}}=\dfrac{\sqrt{6}}{3}a\)
\(HK=\sqrt{AK^2-AH^2}=\sqrt{\dfrac{2}{3}a^2-\dfrac{1}{2}a^2}=\dfrac{\sqrt{6}}{6}a\)
\(S_{AHK}=\dfrac{1}{2}HA.HK=\dfrac{1}{2}\dfrac{\sqrt{2}}{2}a.\dfrac{\sqrt{6}}{6}a=\dfrac{\sqrt{3}}{12}a^2\)
3) AH \(\perp\left(SBC\right)\Rightarrow\left(AK;\left(SBC\right)\right)=\widehat{AKH}\)
\(\Delta AHK\perp\) tại H có : \(sin\widehat{AKH}=\dfrac{AH}{AK}=\dfrac{\sqrt{2}}{2}a:\dfrac{\sqrt{6}}{3}a=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{AKH}=60^o\)






SA vuông góc với (ABC)=> SA vuông góc với BC
mà AB vuông góc với BC ( tam giác ABC vuông)
=> BC vg góc với (SAB)=> BC vg góc AH
mà AH vg góc SB
=> AH vg góc (SBC)=> AH vg góc SC