Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

SA vuông góc với (ABC)=> SA vuông góc với BC
mà AB vuông góc với BC ( tam giác ABC vuông)
=> BC vg góc với (SAB)=> BC vg góc AH
mà AH vg góc SB
=> AH vg góc (SBC)=> AH vg góc SC

Đáp án C
- Ta có:
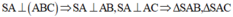 là các tam giác vuông.
là các tam giác vuông.
- Ta có: 
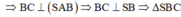 vuông tại B.
vuông tại B.
- Vậy hình chóp đã cho có cả 4 mặt đều là tam giác vuông.

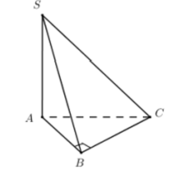
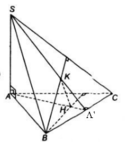
1) Ta có : \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
BC \(\perp AB;BC\perp SA\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) \(\Rightarrow\Delta SBC\perp\) tại B
2) \(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) . Mà
\(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp HK\) \(\Rightarrow\Delta AHK\perp\) tại H
\(\Delta SAB\perp\) tại A ; \(AH\perp SB\) có : \(AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a^2}{\sqrt{2a^2}}=\dfrac{\sqrt{2}}{2}a\)
AC = \(\sqrt{AB^2+BC^2}=\sqrt{2a^2}=\sqrt{2}a\)
\(\Delta SAC\perp\) tại A có : \(AK\perp SC\) có :
\(AK=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a.\sqrt{2}a}{\sqrt{a^2+2a^2}}=\dfrac{\sqrt{6}}{3}a\)
\(HK=\sqrt{AK^2-AH^2}=\sqrt{\dfrac{2}{3}a^2-\dfrac{1}{2}a^2}=\dfrac{\sqrt{6}}{6}a\)
\(S_{AHK}=\dfrac{1}{2}HA.HK=\dfrac{1}{2}\dfrac{\sqrt{2}}{2}a.\dfrac{\sqrt{6}}{6}a=\dfrac{\sqrt{3}}{12}a^2\)
3) AH \(\perp\left(SBC\right)\Rightarrow\left(AK;\left(SBC\right)\right)=\widehat{AKH}\)
\(\Delta AHK\perp\) tại H có : \(sin\widehat{AKH}=\dfrac{AH}{AK}=\dfrac{\sqrt{2}}{2}a:\dfrac{\sqrt{6}}{3}a=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{AKH}=60^o\)

TenAnh1 TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) E = (-3.34, -5.86) E = (-3.34, -5.86) E = (-3.34, -5.86) F = (12.02, -5.86) F = (12.02, -5.86) F = (12.02, -5.86) G = (-3.7, -5.88) G = (-3.7, -5.88) G = (-3.7, -5.88) H = (11.66, -5.88) H = (11.66, -5.88) H = (11.66, -5.88) I = (-3.74, -5.62) I = (-3.74, -5.62) I = (-3.74, -5.62) J = (11.62, -5.62) J = (11.62, -5.62) J = (11.62, -5.62) A'

S A B C H
SH vuông góc (ABC) => AC vuông góc SH, mà AC vuông góc BH nên AC vuông góc (SHB)
=> SB vuông góc AC, kết hợp với SB vuông góc SA => SB vuông góc SC => SA,SB,SC đôi một vuông góc
Từ đó, theo định lì Pytago và BĐT \(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3}\):
\(6\left(SA^2+SB^2+SC^2\right)=3\left(AB^2+BC^2+CA^2\right)\ge3.\frac{\left(AB+BC+CA\right)^2}{3}=\left(AB+BC+CA\right)^2\)

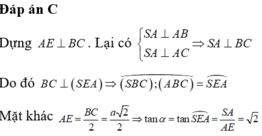




SA vg (ABC)=> SAB,SAC vuông
SA vg BC, AB vg BC => BCvg (SAB) =>SB vg BC=> SBC vuông
vậy all mặt đều vuông
\(\hept{\begin{cases}SA\perp\left(ABC\right)\\AB\subset\left(ABC\right)\end{cases}}\) \(\Rightarrow SA\perp AB\Rightarrow\) tam giác SAB vuông (1)
\(\hept{\begin{cases}SA\perp\left(ABC\right)\\AC\subset\left(ABC\right)\end{cases}\Rightarrow AC\perp SA\Rightarrow}\) tam giác SAC vuông (2)
Tam giác ABC vuông tại B (gt) (3)
\(\Rightarrow AB\perp BC\)
\(\hept{\begin{cases}SA\perp\left(ABC\right)\\BC\subset\left(ABC\right)\end{cases}\Rightarrow SA\perp BC}\)
\(\hept{\begin{cases}AB\perp BC\\SA\perp BC\end{cases}\Rightarrow\hept{\begin{cases}BC\perp\left(SAB\right)\\SB\subset\left(SAB\right)\end{cases}\Rightarrow}SB\perp BC\Rightarrow}\) Tam giác SBC vuông (4)
\(\left(1\right);\left(2\right);\left(3\right);\left(4\right)\Rightarrowđpcm\)