Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

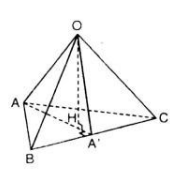
\(\left\{{}\begin{matrix}AO\perp OB\\AO\perp OC\end{matrix}\right.\) \(\Rightarrow AO\perp\left(ABC\right)\Rightarrow OA\perp BC\)
\(OH\perp\left(ABC\right)\Rightarrow OH\perp BC\)
\(\Rightarrow BC\perp\left(OAH\right)\)
b/ \(BC\perp\left(OAH\right)\Rightarrow BC\perp AH\Rightarrow AH\) là 1 đường cao trong tam giác ABC
Chứng minh tương tự câu a ta có\(AC\perp\left(OBH\right)\Rightarrow AC\perp BH\Rightarrow BH\) cùng là 1 đường cao
\(\Rightarrow H\) là trực tâm tam giác ABC
c/ Gọi M là giao điểm AH và BC \(\Rightarrow AM\perp BC\)
Áp dụng hệ thức lượng: \(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OM^2}\) (2)
\(BC\perp\left(OAH\right)\Rightarrow BC\perp OM\Rightarrow OM\) là đường cao ứng với cạnh huyền trong tam giác vuông OBC
Áp dụng hệ thức lượng: \(\frac{1}{OM^2}=\frac{1}{OB^2}+\frac{1}{OC^2}\) (3)
(2);(3) \(\Rightarrow\) đpcm
d/ \(cosA=\frac{AB^2+AC^2-BC^2}{2AB.AC}=\frac{OA^2+OB^2+OA^2+OC^2-\left(OB^2+OC^2\right)}{2AB.AC}=\frac{OA^2}{AB.AC}>0\)
\(\Rightarrow A\) là góc nhọn
Tương tự ta có: \(cosB=\frac{OB^2}{AB.BC}>0\) ; \(cosC=\frac{OC^2}{AC.BC}>0\) nên B, C đều nhọn
Vậy ABC là tam giác nhọn




Đáp án A