Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C
Đáp án D
Từ giả thiết ta thấy 
và OBC là tam giác vuông nên thể tích cần tìm là:
VO.ABC = 1 3 OA.SOBC = 1 6 OA.OB.OC = abc 6
mk nhầm câu c là 25f(x)
câu d là 24f(x)
mk nhầm nũa câu hỏi là cái f(x+2)-f(x) là bỏ nha
Đáp án C
Cách 1.
Gọi N là trung điểm của AC ⇒ M N / / A B
Cho OA =OB =OC =1. Ta có.
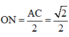
Vậy ∆ O M N là tam giác đều và O M N = 60 o
Cách 2. Dùng pp tọa độ hóa và công thức
Đáp án là A
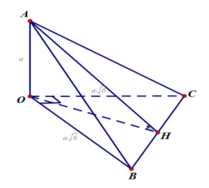
Trong (OBC) kẻ OH ⊥ BC tại H thì có ngay BC ⊥ (OAH)
Do đó :
(vì tam giác OHA vuông tại O nên A H O ^ < 90 o )
Ta có
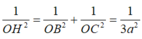
Ta giác OHA vuông tại O nên
Vậy góc giữa hai mặt phẳng (ABC) và (OBC) bằng 30 o
