Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Xác định đoạn vuông góc chung của hai đường thẳng.
Tính độ dài đoạn vuông góc chung.
Cách giải:
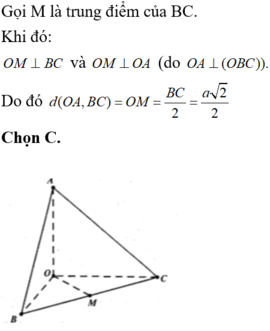
Gọi M là trung điểm của BC.
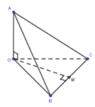
Ta có: 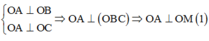
Tam giác OBC: OB = OC => ∆OBC cân tại O, mà M là trung điểm BC ![]()
Từ (1), (2), suy ra: OM là đoạn vuông góc chung của OA và BC => d(OA;BC) = OM
Tam giác OBC vuông tại O, OM là trung tuyến
![]()
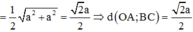

Đáp án C.
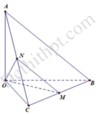
Do OA,OB,OC đội một vuông góc với nhau và O A = O B = O C nên tam giác ABC là tam giác đều. Qua M kẻ đường thẳng song song với AB cắt AC tại N
Ta có M N / / A B ⇒ O M , A B = O M , M N ^ ^
Giả sử O A = O B = O C = a ⇒ A B = B C = C A = a 2
Ta có O M = B C 2 = a 2 2 , O N = A C 2 = a 2 2 , M N = A B 2 = a 2 2
⇒ Δ A B C là tam giác đều ⇒ O M N ^ = 60 0
⇒ O M , M N ^ = 60 0 .

Gọi N là trung điểm của AC ⇒ M N / / A B , Vậy
( OM,AB ) = ( OM,MN ) = OMN
Cho OA = OB = OC = 1. Ta có.
M N = A B 2 = 2 2 O M = B C 2 = 2 2 O N = A C 2 = 2 2
Vậy ∆ O M N là tam giác đều và O M N = 60 o
Đáp án cần chọn là C
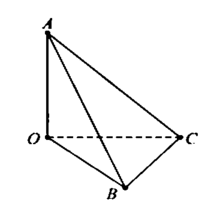 Tính khoảng cách giữa hai đường thẳng AB và OC
Tính khoảng cách giữa hai đường thẳng AB và OC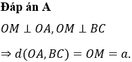
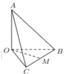
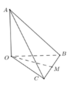


Đáp án B
Ta có O C ⊥ O A O C ⊥ O B ⇒ O C ⊥ O A B
Kẻ O H ⊥ A B ⇒ O C ⊥ O H ⇒ d A B ; O C = O H = O A 2 = a 2 2 .