

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




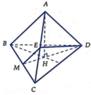
Gọi E là điểm đối xứng M qua A
\(\Rightarrow ANDE\) là hình bình hành (cặp cạnh đối AE và DN song song và bằng nhau)
\(\Rightarrow AN||DE\Rightarrow\) góc giữa AN và SD bằng góc giữa SD và DE
Do tam giác ABD đều \(\Rightarrow MD\perp AB\) \(\Rightarrow\Delta MDE\) vuông tại M
Do tam giác SAB đều \(\Rightarrow SM\perp AB\)
Mà \(\left(SAB\right)\perp\left(ABCD\right)\Rightarrow SM\perp\left(ABCD\right)\)
\(\Rightarrow\) Các tam giác SMD, SME vuông tại M
\(SM=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác SAB đều)
\(MD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác ABD đều)
\(ME=2AM=AB=a\)
Pitago:
\(SD=\sqrt{SM^2+MD^2}=\dfrac{a\sqrt{6}}{2}\)
\(SE=\sqrt{SM^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(ED=\sqrt{MD^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow cos\widehat{SDE}=\dfrac{SD^2+ED^2-SE^2}{2SD.ED}=\dfrac{\sqrt{42}}{14}\)

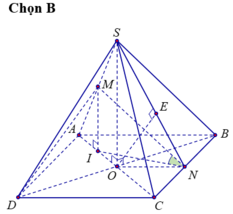
Gọi I là trung điểm OA. Vì IM// SO ⇒ IM⊥(ABCD) nên hình chiếu của MN lên (ABCD) là IN. Suy ra ![]()
Áp dụng định lí cô sin trong ΔCIN, ta có:
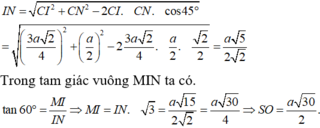
Ta có d(BC, DM) = d(BC, (SAD)) = d(N, (SAD)) = 2d(O, (SAD)) = 2d(O, (SBC)).
Kẻ OE ⊥ SN ⇒ OE ⊥ (SBC).
Ta có d(O, (SBC)) = OE mà
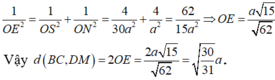

Gọi H là hình chiếu vuông góc của S lên AB, suy ra \(SH\perp\left(ABCD\right)\)
Do đó, SH là đường cao của hình chóp S.BMDN
Ta có : \(SA^2+SB^2=a^2+3a^2=AB^2\)
Nên tam giác SAB là tam giác vuông tại S.
Suy ra : \(SM=\frac{AB}{2}=a\) Do đó tam giác SAM là tam giác đều, suy ra \(SH=\frac{a\sqrt{3}}{3}\)
Diện tích của tứ giác BMDN là \(S_{BMDN}=\frac{1}{2}S_{ABCD}=2a^2\)
Thể tích của khối chóp S.BMDN là \(V=\frac{1}{3}SH.S_{BMDN}=\frac{a^3\sqrt{3}}{3}\)
Kẻ ME song song với DN (E thuộc AD)
Suy ra : \(AE=\frac{a}{2}\) Đặt \(\alpha\) là góc giữa 2 đường thẳng SM và DN
Ta có \(\left(\widehat{SM,ME}\right)=\alpha\), theo định lý 3 đường vuông góc ta có \(SA\perp AE\)
Suy ra :
\(SE=\sqrt{SA^2+AE^2}=\frac{a\sqrt{5}}{2};ME=\sqrt{AM^2+AE^2}=\frac{a\sqrt{5}}{2}\)
Tam giác SME là tam giác cân tại E nên \(\begin{cases}\widehat{SME}=\alpha\\\cos\alpha=\frac{\frac{a}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{5}}{5}\end{cases}\)
Cho mình hỏi, tam giác cân thì tại sao lại suy ra cos góc kia như thế ??